《2025年新课程示径学案作业设计八年级数学上册苏科版》

如图,学校有一块长方形花圃,并在花圃内规划出一条小路。照这样算,走小路比走花圃外围道路少走多少步？(假设 2 步为 1 m)

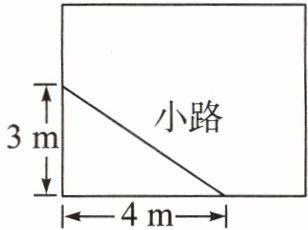
答案： 1. 首先，根据勾股定理$a^{2}+b^{2}=c^{2}$（其中$a = 3m$，$b = 4m$，求小路的长度$c$）：
已知$a = 3m$，$b = 4m$，由勾股定理$c=\sqrt{a^{2}+b^{2}}$，则$c=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5m$。
2. 然后，计算走花圃外围道路比走小路多的长度：
走花圃外围道路的长度为$3 + 4$，走小路长度为$5m$，那么多走的长度$\Delta l=(3 + 4)-5=2m$。
3. 最后，根据$2$步为$1m$计算多走的步数：
因为$2$步为$1m$，所以多走的步数$n = 2×2=4$步。
答：走小路比走花圃外围道路少走$4$步。

例 1 《九章算术》中有一个“折竹”问题：“今有竹高一丈,末折抵地,去根三尺,问折者高几何？”题意是：一根竹子原高 1 丈(1 丈 = 10 尺),中部有一处折断,竹梢触地面处离竹根 3 尺,折断处离地面多高？

答案： 设折断处离地面的高度为$ x $尺，则折断部分的长度为$ (10 - x) $尺。
根据勾股定理，得$ x^2 + 3^2 = (10 - x)^2 $。
展开方程右边：$ x^2 + 9 = 100 - 20x + x^2 $。
移项化简：$ 20x = 91 $。
解得$ x = \frac{91}{20} = 4.55 $。
答：折断处离地面$ 4.55 $尺。

同质训练 1 《算法统宗》中记载了这样一道题：平地秋千未起,踏板一尺离地。送行二步恰竿齐,五尺板高离地。大致意思如下：如图,秋千 $ OA $ 静止的时候,踏板离地高一尺($ AC = 1 $ 尺)。将秋千往前推进两步($ EB = 10 $ 尺)。此时踏板离地五尺($ BD = 5 $ 尺)。求秋千绳索($ OA $ 或 $ OB $)的长。(尺是古代长度单位)

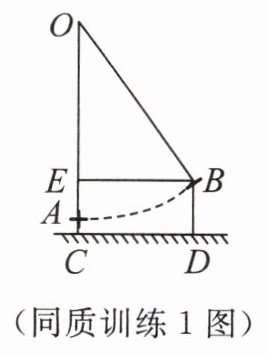
答案： 设秋千绳索长 $x$ 尺，
由题意，$OA=OB=x$，
$AE = BD - AC=5 - 1 = 4$（尺），
$BE = 10$（尺），
$OE = OA - AE = x - 4$（尺），
在$Rt \bigtriangleup OBE$中，
由勾股定理得：
$OB^2 = BE^2 + OE^2$，
即$x^2 = 10^2 + (x - 4)^2$，
$x^2 = 100 + x^2 - 8x + 16$，
$8x = 116$，
解得$x = 14.5$。
所以秋千绳索长$14.5$尺。