《2025年新课程示径学案作业设计八年级数学上册苏科版》

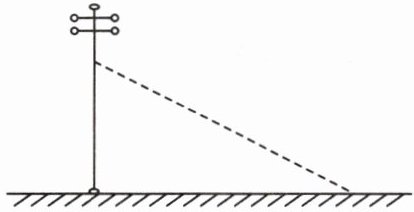
如图,从电线杆离地面6m处向地面拉一条长10m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有多远？

答案： 设缆绳在地面的固定点距离电线杆底部有$x$米。
由题意知，电线杆垂直于地面，所以构成直角三角形，其中电线杆离地面的高度$6m$和固定点到电线杆底部的距离$x$为直角边，缆绳长$10m$为斜边。
根据勾股定理：$x^{2}+6^{2}=10^{2}$
$x^{2}+36=100$
$x^{2}=100 - 36$
$x^{2}=64$
$x = 8$（负值舍去）
答：这条缆绳在地面的固定点距离电线杆底部有$8m$。

例1 如图①,点P在直线l外,PA⊥直线l,垂足为A,Q为直线l上不同于点A的任意一点.求证：PA＜PQ.小明的操作如下：如图①,延长PA至点B,使得AB= PA,连接BQ……
(1)请接着小明的操作完成证明；
(2)小芳发现还可以通过“勾股定理”来证明,请结合图②完成.

答案：
(1)
∵PA⊥直线l，
∴∠PAQ=90°。延长PA至点B，使AB=PA，则PB=PA+AB=2PA，且l垂直平分线段PB。
∵Q在直线l上，
∴由垂直平分线性质得QP=QB。在△PBQ中，PQ+QB＞PB（三角形两边之和大于第三边），又QB=QP，
∴2PQ＞2PA，
∴PQ＞PA，即PA＜PQ。
(2)
∵PA⊥直线l，
∴△PAQ为直角三角形，∠PAQ=90°。由勾股定理得PQ²=PA²+AQ²。
∵Q≠A，
∴AQ＞0，
∴AQ²＞0，
∴PQ²＞PA²。
∵PQ＞0，PA＞0，
∴PQ＞PA，即PA＜PQ。