第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
如图,∠1= ∠2,请你添加一个条件,求证:BD= CD.
(1) 请写出三种添加一个条件的方案;
(2) 选择一种添加条件的方案,然后写出证明过程.
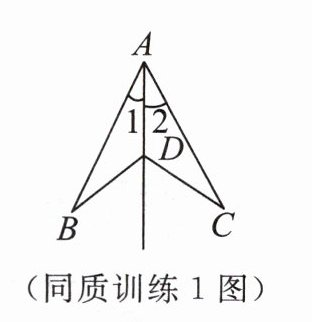
(1) 请写出三种添加一个条件的方案;
(2) 选择一种添加条件的方案,然后写出证明过程.

答案:
(1) 方案一:添加条件 $AB = AC$;
方案二:添加条件 $\angle B = \angle C$;
方案三:添加条件 $AD \perp BC$。
(2) 选择方案一:添加条件 $AB = AC$。
证明:
在$\triangle ABD$和$\triangle ACD$中,
$\begin{cases}AB = AC, \\\angle 1 = \angle 2, \\AD = AD.\end{cases}$
根据$SAS$(两边及夹角)全等条件,
$\therefore \triangle ABD \cong \triangle ACD$,
根据全等三角形的对应边相等,
$\therefore BD = CD$。
(1) 方案一:添加条件 $AB = AC$;
方案二:添加条件 $\angle B = \angle C$;
方案三:添加条件 $AD \perp BC$。
(2) 选择方案一:添加条件 $AB = AC$。
证明:
在$\triangle ABD$和$\triangle ACD$中,
$\begin{cases}AB = AC, \\\angle 1 = \angle 2, \\AD = AD.\end{cases}$
根据$SAS$(两边及夹角)全等条件,
$\therefore \triangle ABD \cong \triangle ACD$,
根据全等三角形的对应边相等,
$\therefore BD = CD$。
例 2
如图,在△ABC 中,EF 垂直平分 AC,交 AC 于点 F,交 BC 于点 E,AD⊥BC,垂足为 D,且 BD= DE,连接 AE.
(1) 求证:AB= EC;
(2) 若△ABC 的周长为 19 cm,AC= 8 cm,求 DC 的长.

如图,在△ABC 中,EF 垂直平分 AC,交 AC 于点 F,交 BC 于点 E,AD⊥BC,垂足为 D,且 BD= DE,连接 AE.
(1) 求证:AB= EC;
(2) 若△ABC 的周长为 19 cm,AC= 8 cm,求 DC 的长.

答案:
(1) 见证明过程;
(2) 5.5cm。
(1) 见证明过程;
(2) 5.5cm。
如图,在△ABC 中,AB 的垂直平分线 EF 交 BC 于点 E,交 AB 于点 F,D 为线段 CE 的中点,BE= AC.
(1) 求证:AD⊥BC;
(2) 若∠B= 35°,求∠C 的度数.

(1) 求证:AD⊥BC;
(2) 若∠B= 35°,求∠C 的度数.

答案:
(1) 见上述证明;
(2) 70°
(1) 见上述证明;
(2) 70°
例 3
如图,∠AOC 和∠BOD 共顶点,∠BOD 为直角,OC 是∠BOD 的平分线,∠AOB= 150°.
(1) 求∠AOC 的度数;
(2) 若∠BOE:∠AOD= 2:3,求∠COE 的度数.

如图,∠AOC 和∠BOD 共顶点,∠BOD 为直角,OC 是∠BOD 的平分线,∠AOB= 150°.
(1) 求∠AOC 的度数;
(2) 若∠BOE:∠AOD= 2:3,求∠COE 的度数.

答案:
(1)
∵∠BOD为直角,
∴∠BOD=90°.
∵OC是∠BOD的平分线,
∴∠BOC=∠COD=45°.
∵∠AOB=150°,∠AOB=∠AOD+∠DOB,∠DOB=90°,
∴∠AOD=∠AOB-∠DOB=150°-90°=60°.
∴∠AOC=∠AOD+∠DOC=60°+45°=105°.
(2)
∵∠BOE:∠AOD=2:3,∠AOD=60°,
∴∠BOE=(2/3)×60°=40°.
当OE在∠BOC内部时,∠COE=∠BOC-∠BOE=45°-40°=5°;
当OE在∠BOC外部(OB下方)时,∠COE=∠BOC+∠BOE=45°+40°=85°.
综上,∠COE=5°或85°.
(1)
∵∠BOD为直角,
∴∠BOD=90°.
∵OC是∠BOD的平分线,
∴∠BOC=∠COD=45°.
∵∠AOB=150°,∠AOB=∠AOD+∠DOB,∠DOB=90°,
∴∠AOD=∠AOB-∠DOB=150°-90°=60°.
∴∠AOC=∠AOD+∠DOC=60°+45°=105°.
(2)
∵∠BOE:∠AOD=2:3,∠AOD=60°,
∴∠BOE=(2/3)×60°=40°.
当OE在∠BOC内部时,∠COE=∠BOC-∠BOE=45°-40°=5°;
当OE在∠BOC外部(OB下方)时,∠COE=∠BOC+∠BOE=45°+40°=85°.
综上,∠COE=5°或85°.
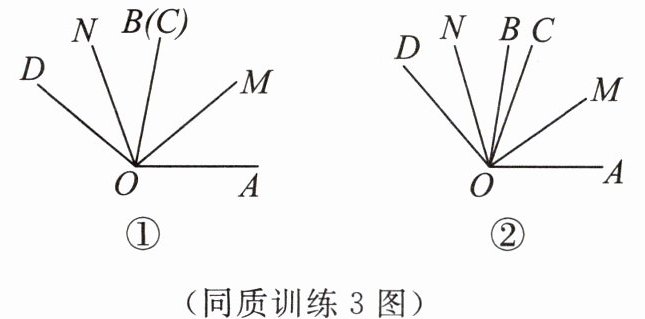
已知∠AOB= 80°,∠COD= 60°,OM,ON 分别平分∠AOC,∠BOD.
(1) 如图①,当 OB 与 OC 重合时,∠MON 的度数是
(2) 若图①中∠AOB 不动,将∠COD 从图①的位置开始绕点 O 顺时针旋转.
① 如图②,当∠BOC= 10°时,求∠MON 的度数;
② 当∠BOC= α(60°<α<80°)时,直接用等式表示∠AOM 与∠DON 的数量关系.
(1) 如图①,当 OB 与 OC 重合时,∠MON 的度数是
70°
;(2) 若图①中∠AOB 不动,将∠COD 从图①的位置开始绕点 O 顺时针旋转.
① 如图②,当∠BOC= 10°时,求∠MON 的度数;
② 当∠BOC= α(60°<α<80°)时,直接用等式表示∠AOM 与∠DON 的数量关系.

答案:
(1) 70°
(2) ①
∵∠AOB=80°,∠BOC=10°,
∴∠AOC=∠AOB - ∠BOC=70°
∵OM平分∠AOC,
∴∠MOC=∠AOC/2=35°
∵∠COD=60°,∠BOC=10°,
∴∠BOD=∠COD - ∠BOC=50°
∵ON平分∠BOD,
∴∠BON=∠BOD/2=25°
∵∠MON=∠MOC + ∠BOC + ∠BON=35°+10°+25°=70°
② ∠AOM + ∠DON=10°
(1) 70°
(2) ①
∵∠AOB=80°,∠BOC=10°,
∴∠AOC=∠AOB - ∠BOC=70°
∵OM平分∠AOC,
∴∠MOC=∠AOC/2=35°
∵∠COD=60°,∠BOC=10°,
∴∠BOD=∠COD - ∠BOC=50°
∵ON平分∠BOD,
∴∠BON=∠BOD/2=25°
∵∠MON=∠MOC + ∠BOC + ∠BON=35°+10°+25°=70°
② ∠AOM + ∠DON=10°
查看更多完整答案,请扫码查看


