《2025年新课程示径学案作业设计八年级数学上册苏科版》

例 如果一个点到一条线段两端的距离相等,那么这个点是否在这条线段的垂直平分线上呢？

答案： 已知：点P是线段AB外一点，且PA=PB；或点P是线段AB上一点，且PA=PB。
求证：点P在AB的垂直平分线上。
证明：
情况1：当点P在线段AB上时，
∵PA=PB，
∴点P是线段AB的中点，
∵线段中点在其垂直平分线上，
∴点P在AB的垂直平分线上。
情况2：当点P不在线段AB上时，
过点P作PO⊥AB于点O，
在Rt△PAO和Rt△PBO中，
∵PA=PB，PO=PO，
∴Rt△PAO≌Rt△PBO（HL），
∴AO=BO，
∵PO⊥AB且AO=BO，
∴PO是AB的垂直平分线，
∴点P在AB的垂直平分线上。
综上，点P在AB的垂直平分线上。
结论：这个点在这条线段的垂直平分线上。

归纳小结：到线段两端距离相等；线段的垂直平分线是到线段两端距离相等的点的集合.
符号语言：

答案： 1. 首先分析第一个空：
根据线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等。
2. 然后分析第二个空：
根据线段垂直平分线的判定定理：到一条线段的两个端点的距离相等的点，在这条线段的垂直平分线上。所以线段的垂直平分线是到线段两端距离相等的点的集合。
故答案依次为：距离相等；到线段两端距离相等。

同质训练 如图,利用网格在图中找一点 $ O $,使 $ OA = OB = OC $.

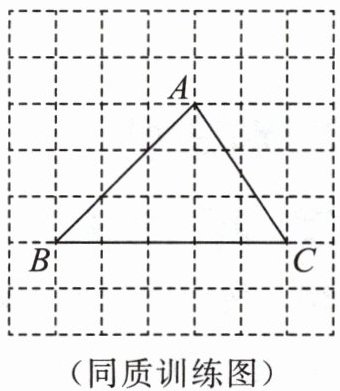
答案： 1. 作线段BC的垂直平分线：
找到BC的中点（BC为水平线段，中点为BC中间格点）；
过中点作垂直于BC的直线（竖直线）。
2. 作线段AB的垂直平分线：
找到AB的中点（AB为斜线段，中点为横纵方向中间格点）；
过中点作垂直于AB的直线（根据网格斜率确定方向，如斜率为-1的直线）。
3. 两垂直平分线的交点即为点O。
结论：点O为网格中两垂直平分线的交点（具体位置在网格第3列第1行格点处，假设网格小正方形边长为1）。

例 如图,在 $ \triangle ABC $ 中,$ AB $,$ AC $ 的垂直平分线 $ l_1 $,$ l_2 $ 相交于点 $ O $.求证：点 $ O $ 在 $ BC $ 的垂直平分线上.

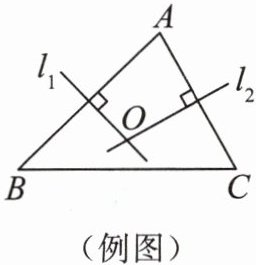
答案： 证明：
连接$OA$，$OB$，$OC$，
$\because l_1$是$AB$的垂直平分线，
$\therefore OA = OB$。
$\because l_2$是$AC$的垂直平分线，
$\therefore OA = OC$，
$\therefore OB = OC$，
$\therefore$点$O$在$BC$的垂直平分线上。

同质训练 课本 $ P35 $ 讨论：如图,$ AB = AD $,$ CB = CD $,$ AC $,$ BD $ 相交于点 $ E $.你能在图中找到哪些相等的角？如何证明？

答案： 相等的角有：∠AEB=∠AED=∠CEB=∠CED，∠BAC=∠DAC，∠BCA=∠DCA，∠ABC=∠ADC，∠ABE=∠ADE，∠CBE=∠CDE。
证明：
1. 证AC是BD的垂直平分线

∵AB=AD，
∴点A在线段BD的垂直平分线上（到线段两端距离相等的点在垂直平分线上）。

∵CB=CD，
∴点C在线段BD的垂直平分线上。

∵两点确定一条直线，
∴直线AC垂直平分BD。

∴BE=DE，AC⊥BD，即∠AEB=∠AED=∠CEB=∠CED=90°。
2. 证△ABC≌△ADC
在△ABC和△ADC中，
$\left\{\begin{array}{l}AB=AD\\ CB=CD\\ AC=AC\end{array}\right.$

∴△ABC≌△ADC（SSS）。

∴∠BAC=∠DAC，∠BCA=∠DCA，∠ABC=∠ADC（全等三角形对应角相等）。
3. 证△ABE≌△ADE
在△ABE和△ADE中，
$\left\{\begin{array}{l}AB=AD\\ AE=AE\\ BE=DE\end{array}\right.$

∴△ABE≌△ADE（SSS）。

∴∠ABE=∠ADE（全等三角形对应角相等）。
4. 证△CBE≌△CDE
在△CBE和△CDE中，
$\left\{\begin{array}{l}CB=CD\\ CE=CE\\ BE=DE\end{array}\right.$

∴△CBE≌△CDE（SSS）。

∴∠CBE=∠CDE（全等三角形对应角相等）。
综上，图中相等的角为：∠AEB=∠AED=∠CEB=∠CED，∠BAC=∠DAC，∠BCA=∠DCA，∠ABC=∠ADC，∠ABE=∠ADE，∠CBE=∠CDE。