第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
例 2 小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程 $s$(单位:$\mathrm{km}$)与所用时间 $t$(单位:$\mathrm{h}$)之间的关系. 试根据图象回答下列问题.
(1) 小明从甲地到乙地用了多少时间?
(2) 小明出发 $5\mathrm{h}$ 时,距离甲地有多远?
(3) 折线中有一条平行于横轴的线段,它的实际意义是什么?
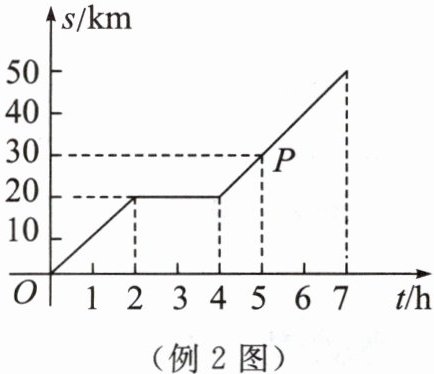
(1) 小明从甲地到乙地用了多少时间?
(2) 小明出发 $5\mathrm{h}$ 时,距离甲地有多远?
(3) 折线中有一条平行于横轴的线段,它的实际意义是什么?

答案:
(1) 由图象可知,当 $s = 50\mathrm{km}$ 时,对应的 $t = 7\mathrm{h}$,所以小明从甲地到乙地用了 $7\mathrm{h}$。
(2) 由图象可知,当 $t = 5\mathrm{h}$ 时,对应的 $s = 30\mathrm{km}$,所以小明出发 $5\mathrm{h}$ 时,距离甲地 $30\mathrm{km}$。
(3) 折线中平行于横轴的线段的实际意义是:小明在 $2\mathrm{h}$ 到 $4\mathrm{h}$ 这个时间段内处于静止状态(或休息状态)。
(1) 由图象可知,当 $s = 50\mathrm{km}$ 时,对应的 $t = 7\mathrm{h}$,所以小明从甲地到乙地用了 $7\mathrm{h}$。
(2) 由图象可知,当 $t = 5\mathrm{h}$ 时,对应的 $s = 30\mathrm{km}$,所以小明出发 $5\mathrm{h}$ 时,距离甲地 $30\mathrm{km}$。
(3) 折线中平行于横轴的线段的实际意义是:小明在 $2\mathrm{h}$ 到 $4\mathrm{h}$ 这个时间段内处于静止状态(或休息状态)。
同质训练 2 某剧院的观众席的座位为扇形,按相同的规律排列. 下表记录了前 $5$ 排的座位数.

(1) 按照上表所示的规律,当 $x$ 每增加 $1$ 时,$y$ 如何变化?
(2) 座位数 $y$ 是否为排数 $x$ 的函数?若是,请写出一个符合表中数据的函数表达式.
(3) 按照上表所示的规律,某一排可能有 $90$ 个座位吗?说说你的理由.

(1) 按照上表所示的规律,当 $x$ 每增加 $1$ 时,$y$ 如何变化?
(2) 座位数 $y$ 是否为排数 $x$ 的函数?若是,请写出一个符合表中数据的函数表达式.
(3) 按照上表所示的规律,某一排可能有 $90$ 个座位吗?说说你的理由.
答案:
(1)由表可知,当$x$从$1$变到$2$时,$y$从$50$变到$53$,增加$3$;$x$从$2$变到$3$时,$y$从$53$变到$56$,增加$3$,以此类推,当$x$每增加$1$时,$y$增加$3$。
(2)是。
设函数表达式为$y = kx + b$,把$x = 1$,$y = 50$;$x = 2$,$y = 53$代入得$\begin{cases}k + b = 50\\2k + b = 53\end{cases}$
两式相减得$k = 3$,把$k = 3$代入$k + b = 50$得$b = 47$,所以$y = 3x + 47$。
(3)假设某一排可能有$90$个座位,则$3x + 47 = 90$,$3x = 43$,$x=\frac{43}{3}\approx14.33$,不是整数,所以某一排不可能有$90$个座位。
(1)由表可知,当$x$从$1$变到$2$时,$y$从$50$变到$53$,增加$3$;$x$从$2$变到$3$时,$y$从$53$变到$56$,增加$3$,以此类推,当$x$每增加$1$时,$y$增加$3$。
(2)是。
设函数表达式为$y = kx + b$,把$x = 1$,$y = 50$;$x = 2$,$y = 53$代入得$\begin{cases}k + b = 50\\2k + b = 53\end{cases}$
两式相减得$k = 3$,把$k = 3$代入$k + b = 50$得$b = 47$,所以$y = 3x + 47$。
(3)假设某一排可能有$90$个座位,则$3x + 47 = 90$,$3x = 43$,$x=\frac{43}{3}\approx14.33$,不是整数,所以某一排不可能有$90$个座位。
归纳小结:函数有三种表示方法:
(1) 列表法.
① 自变量的取值写在第一行,对应的函数值写在第二行,用
② 列表法容易看出函数值和
(2) 表达式法.
① 用
② 表达式法比较简洁,方便
(3) 图象法.
① 把自变量的取值作为横坐标,对应的函数值作为
② 图象法能够直观地看到变化
列表法
、表达式法
和图象法
.(1) 列表法.
① 自变量的取值写在第一行,对应的函数值写在第二行,用
表格
的形式列出部分自变量的值
和相应的函数值
的方法.② 列表法容易看出函数值和
自变量
的关系.(2) 表达式法.
① 用
含自变量的代数式
和运算符号
组成的表示函数的表达式叫作函数表达式.② 表达式法比较简洁,方便
计算函数值
.(3) 图象法.
① 把自变量的取值作为横坐标,对应的函数值作为
纵坐标
,在平面直角坐标系中描出相应的点
,这些点组成的图形叫作函数的图象.② 图象法能够直观地看到变化
趋势
.
答案:
列表法;表达式法;图象法;
(1)①表格;自变量的值;函数值;②自变量;
(2)①含自变量的代数式;运算符号;②计算函数值;
(3)①纵坐标;点;②趋势
(1)①表格;自变量的值;函数值;②自变量;
(2)①含自变量的代数式;运算符号;②计算函数值;
(3)①纵坐标;点;②趋势
查看更多完整答案,请扫码查看


