《2025年新课程示径学案作业设计八年级数学上册苏科版》

例 2 甲、乙两种款式手机屏幕的对角线长分别为 5.5 英寸和 5.4 英寸,纵横比分别为 $ 2:1 $ 和 $ 16:9 $,哪款手机的屏幕面积更大？(1 英寸 $ \approx 2.54 cm $)

答案： 设甲手机屏幕长为$2x$英寸，宽为$x$英寸（纵横比$2:1$），对角线$5.5$英寸。由勾股定理：
$(2x)^2 + x^2 = 5.5^2$，即$5x^2 = 30.25$，解得$x^2 = 6.05$。
甲面积$= 2x \cdot x = 2x^2 = 2 × 6.05 = 12.1$（平方英寸）。
设乙手机屏幕长为$16y$英寸，宽为$9y$英寸（纵横比$16:9$），对角线$5.4$英寸。由勾股定理：
$(16y)^2 + (9y)^2 = 5.4^2$，即$337y^2 = 29.16$，解得$y^2 = \frac{29.16}{337}$。
乙面积$= 16y \cdot 9y = 144y^2 = 144 × \frac{29.16}{337} \approx 144 × 0.0865 = 12.46$（平方英寸）。
因为$12.46 ＞ 12.1$，所以乙款手机屏幕面积更大。
结论：乙款手机的屏幕面积更大。

同质训练 2 在一次消防演习中,一架长 20 m 的云梯斜靠在一面墙上,云梯底端离墙 12 m。
(1)这架云梯的顶端距地面有多高？
(2)如果要求云梯的顶端下降 4 m(云梯长度不变),那么云梯的底部在水平方向应滑动多少米？

答案：
(1)设云梯顶端距地面高度为$h$米，云梯长度为斜边$20$米，底端离墙距离为直角边$12$米。根据勾股定理$h^2 + 12^2 = 20^2$，$h^2 = 400 - 144 = 256$，解得$h = 16$。
(2)顶端下降$4$米后高度为$16 - 4 = 12$米，设此时底端离墙距离为$x$米。由勾股定理$12^2 + x^2 = 20^2$，$x^2 = 400 - 144 = 256$，解得$x = 16$。滑动距离为$16 - 12 = 4$米。
(1)16米；
(2)4米。

例 3 如图,笔直的河流一侧有一个旅游景点 $ C $,河边有两个游船码头 $ A $,$ B $,其中 $ AB = AC $。因为旅游景点 $ C $ 到游船码头 $ A $ 的路不通,为方便游客,相关部门决定在河边新建一个游船码头 $ D $,并修建一条路 $ CD $,测得 $ BC = 5 km $,$ CD = 4 km $,$ BD = 3 km $。求原来的路线 $ AC $ 的长。

答案： 设AC的长为$ x \, km $，因为$ AB = AC $，所以$ AB = x \, km $。
在$ \triangle CDB $中，$ CD = 4 \, km $，$ BD = 3 \, km $，$ BC = 5 \, km $。
由于$ BD^2 + CD^2 = 3^2 + 4^2 = 9 + 16 = 25 = 5^2 = BC^2 $，
所以$ \triangle CDB $是直角三角形，且$ \angle CDB = 90° $，即$ CD \perp AB $。
设$ AD = y \, km $，因为$ A $，$ D $，$ B $在同一直线上，且$ D $在$ A $，$ B $之间，所以$ AB = AD + DB $，即$ x = y + 3 $，故$ y = x - 3 $。
在$ Rt\triangle CDA $中，$ AC^2 = AD^2 + CD^2 $，即$ x^2 = y^2 + 4^2 $。
将$ y = x - 3 $代入，得$ x^2 = (x - 3)^2 + 16 $。
展开得$ x^2 = x^2 - 6x + 9 + 16 $，
化简得$ 0 = -6x + 25 $，解得$ x = \frac{25}{6} $。
答：原来的路线$ AC $的长为$ \frac{25}{6} \, km $。

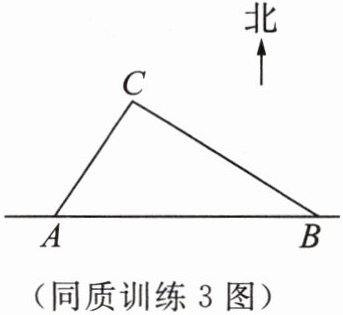
同质训练 3 台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向 $ AB $ 由点 $ A $ 移动至点 $ B $。已知点 $ C $ 为一海港,且点 $ C $ 与直线 $ AB $ 上两点 $ A $,$ B $ 的距离分别为 300 km 和 400 km,又 $ AB = 500 km $,以台风中心为圆心周围 250 km 以内为受影响区域。
(1)海港 $ C $ 受台风影响吗？为什么？
(2)若台风的速度为 20 km/h,则台风影响该海港持续的时间有多长？

答案：
(1)受影响；
(2)7小时。