《2025年新课程示径学案作业设计八年级数学上册苏科版》

线段是轴对称图形吗？它的对称轴是什么？

答案： 线段是轴对称图形，它的对称轴是线段的垂直平分线和线段本身所在的直线。

例 按照下列要求画图：
① 任意画一条线段 $ AB $；
② 画出线段 $ AB $ 的垂直平分线 $ l $,并与线段 $ AB $ 相交于点 $ O $；
③ 在直线 $ l $ 上任意取一点 $ P $,连接 $ PA $,$ PB $.
探究：线段 $ PA $ 与 $ PB $ 相等吗？如何证明？请在下方写出证明过程.

答案： 答题：
① 画一条线段 $ AB $。
② 画出线段 $ AB $ 的垂直平分线 $ l $，并与线段 $ AB $ 相交于点 $ O $。
③ 在直线 $ l $ 上任意取一点 $ P $，连接 $ PA $ 和 $ PB $。
证明过程：
由于 $ l $ 是 $ AB $ 的垂直平分线，根据垂直平分线的定义，有 $ OA = OB $，且 $ l \perp AB $。
在 $\triangle POA$ 和 $\triangle POB$ 中：
$ OA = OB $（因为 $ l $ 是 $ AB $ 的垂直平分线），
$ \angle POA = \angle POB = 90° $（因为 $ l \perp AB $），
$ OP = OP $（公共边）。
根据三角形的全等判定——SAS（边-角-边）全等条件，有 $\triangle POA \cong \triangle POB$。
由于 $\triangle POA \cong \triangle POB$，根据全等三角形的对应边相等，得出 $ PA = PB $。
结论：线段 $ PA $ 与 $ PB $ 相等。

归纳小结：线段垂直平分线上的点到这条线段两个端点的距离相等.
符号语言：

答案： 到这条线段两个端点的距离相等

同质训练 如图,$ DE $ 是 $ \triangle ABC $ 的边 $ AC $ 的垂直平分线.已知 $ BC = 8 $,$ AB = 10 $,求 $ \triangle EBC $ 的周长.

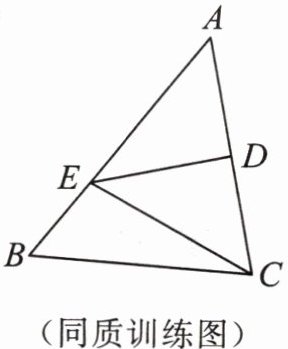
答案：
∵DE是△ABC的边AC的垂直平分线，
∴EA=EC（线段垂直平分线上的点到线段两端距离相等）。
∵BC=8，AB=10，
∴△EBC的周长=EB+EC+BC=EB+EA+BC=AB+BC=10+8=18。
答：△EBC的周长为18。