《2025年新课程示径学案作业设计八年级数学上册苏科版》

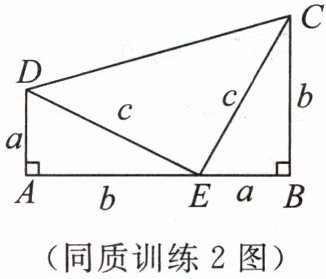
同质训练 2 如图,$\mathrm{Rt}\triangle ADE和\mathrm{Rt}\triangle BEC$是完全相同的三角形,点$A,E,B$在同一条直线上.请用此图形验证勾股定理.(要验证$a,b,c$之间的关系,应从直角梯形的面积入手)

答案：
∵Rt△ADE≌Rt△BEC，∠A=∠B=90°，设AD=BC=a，AE=BE=b，DE=EC=c，点A,E,B共线，
∴AB=AE+BE=a+b，AD//BC，四边形ABCD为直角梯形。
方法一：梯形面积公式
S_梯形ABCD=$\frac{1}{2}$(AD+BC)·AB=$\frac{1}{2}$(a+b)(a+b)=$\frac{(a+b)^2}{2}$。
方法二：分割为三个三角形面积之和
S_梯形ABCD=S_△ADE+S_△BEC+S_△DEC。
∵S_△ADE=S_△BEC=$\frac{1}{2}$ab，
∴S_△ADE+S_△BEC=ab。
∵∠AED+∠ADE=90°，∠ADE=∠BEC（全等三角形对应角相等），
∴∠AED+∠BEC=90°，
∴∠DEC=180°-90°=90°。
∴S_△DEC=$\frac{1}{2}$DE·EC=$\frac{1}{2}$c²。
故S_梯形ABCD=ab+$\frac{1}{2}$c²。
由面积相等得
$\frac{(a+b)^2}{2}$=ab+$\frac{1}{2}$c²，
化简得a²+2ab+b²=2ab+c²，
∴a²+b²=c²。
即验证勾股定理。

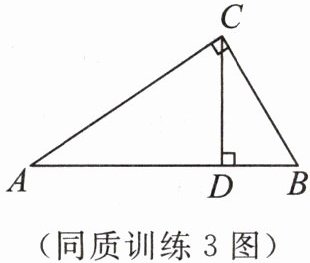
同质训练 3 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$CD\perp AB$,垂足为$D$,$AC= 12$,$BC= 9$,求$CD$的长.

答案： $CD$的长为$\frac{36}{5}$（或$7.2$）。

问题二 如何运用勾股定理解决实际问题?
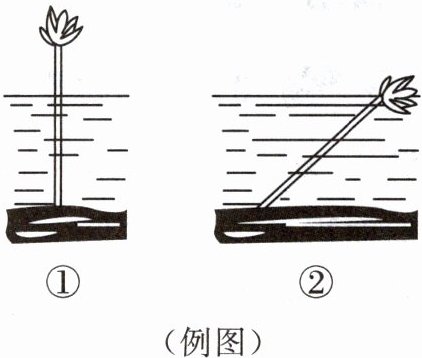
例 如图①,波平如静的湖面上有一朵美丽的红莲,它高出水面$1\mathrm{m}$.一阵大风吹过,红莲被吹至一边,花朵齐及水面(如图②).如果知道红莲移动的水平距离为$2\mathrm{m}$,那么这里水深多少?

答案： 设水深为$x\ m$，则红莲的长度为$(x + 1)\ m$。
红莲被吹倒后，水深$x\ m$、水平移动距离$2\ m$与红莲长度$(x + 1)\ m$构成直角三角形，其中红莲长度为斜边。
由勾股定理得：$x^2 + 2^2=(x + 1)^2$。
展开右边：$x^2 + 4=x^2 + 2x + 1$。
移项化简：$2x=3$，解得$x = 1.5$。
答：水深为$1.5\ m$。

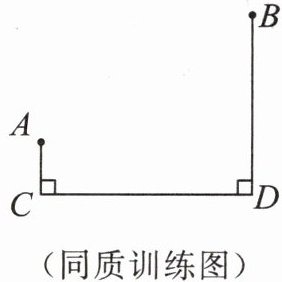
同质训练 如图,$A,B两村庄在笔直的小河CD$的同侧,$A,B两村庄到河的距离分别为AC= 1\mathrm{km}$,$BD= 3\mathrm{km}$,$CD= 3\mathrm{km}$.现要在河边$CD上建一水厂向A,B$两村庄输送自来水,且铺设管道的工程费用为每千米$2$万元.请在小河$CD$上选择水厂的位置,使铺设水管的费用最节省,并求出铺设水管的总费用.

答案： 解：
1. 作对称点：作点A关于直线CD的对称点A'，则A'C=AC=1km，且A'在CD另一侧。
2. 确定最短路径：连接A'B，交CD于点P，此时PA+PB最小（依据：两点之间线段最短，PA=PA'）。
3. 计算A'B长度：过A'作A'E⊥BD交BD延长线于E，易知A'E=CD=3km，BE=BD+A'C=3+1=4km。
在Rt△A'EB中，由勾股定理得：
$ A'B = \sqrt{A'E^2 + BE^2} = \sqrt{3^2 + 4^2} = 5 \, km $。
4. 总费用：铺设水管总长度为5km，费用为 $ 5 × 2 = 10 \, 万元 $。
答：水厂建在A'B与CD的交点处，总费用为10万元。