《2025年新课程示径学案作业设计八年级数学上册苏科版》

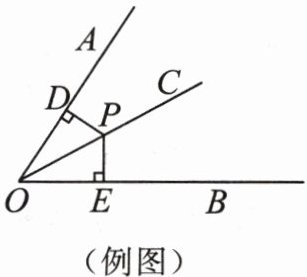
例 如图,点$P在\angle AOB$的内部,$PD\perp OA$,$PE\perp OB$,垂足分别为$D$,$E$,$PD = PE$.那么点$P在\angle AOB$的平分线上吗？

归纳小结：角的内部到角两边距离相等的点在角的平分线上.角的平分线是到角两边距离相等的点的集合.
几何语言：∵点P在∠AOB的内部，PD⊥OA，PE⊥OB，PD=PE，∴点P在∠AOB的平分线上。

答案： 点P在∠AOB的平分线上。
证明：连接OP。
∵PD⊥OA，PE⊥OB，
∴∠PDO=∠PEO=90°。
在Rt△PDO和Rt△PEO中，
OP=OP，PD=PE，
∴Rt△PDO≌Rt△PEO（HL）。
∴∠DOP=∠EOP。
∴OP是∠AOB的平分线，即点P在∠AOB的平分线上。
归纳小结：角的内部到角两边距离相等的点在角的平分线上。角的平分线是到角两边距离相等的点的集合。
几何语言：
∵点P在∠AOB的内部，PD⊥OA，PE⊥OB，PD=PE，
∴点P在∠AOB的平分线上。

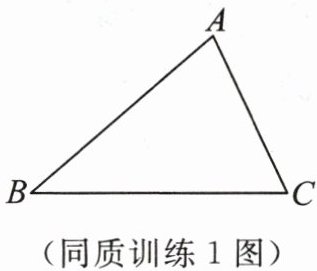
同质训练 $1$ 如图,已知$\triangle ABC$,先作出$\angle B$,$\angle C$的平分线,相交于点$O$,连接$OA$.求证：$OA平分\angle BAC$.

答案： 证明：过点O作OD⊥AB于D，OE⊥BC于E，OF⊥AC于F。
∵BO平分∠ABC，OD⊥AB，OE⊥BC，
∴OD=OE（角平分线上的点到角两边距离相等）。
同理，
∵CO平分∠ACB，OE⊥BC，OF⊥AC，
∴OE=OF。
∴OD=OF。
∵OD⊥AB，OF⊥AC，
∴OA平分∠BAC（到角两边距离相等的点在角的平分线上）。

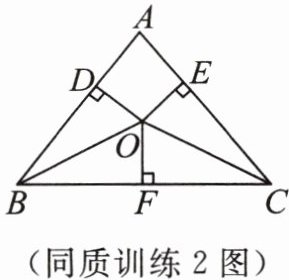
同质训练 $2$ 如图,在$\triangle ABC$中,$O为\angle ABC$,$\angle ACB$平分线的交点,$OD\perp AB$,$OE\perp AC$,$OF\perp BC$,垂足分别为$D$,$E$,$F$.
(1) $OD与OE$是否相等？请说明理由.
(2) 若$\triangle ABC的周长是30$,且$OF = 3$,求$\triangle ABC$的面积.

答案：
(1) $OD = OE$，理由如下：
因为$OB$，$OC$分别是$\angle ABC$，$\angle ACB$的平分线，$OD\perp AB$，$OF\perp BC$，根据角平分线的性质：角平分线上的点到角两边的距离相等，所以$OD = OF$；同理$OE = OF$。
所以$OD = OE$。
(2)
因为$OD = OE = OF$，$OD\perp AB$，$OE\perp AC$，$OF\perp BC$，$\triangle ABC$周长为$30$。
$S_{\triangle ABC}=S_{\triangle ABO}+S_{\triangle BCO}+S_{\triangle ACO}=\frac{1}{2}AB\cdot OD+\frac{1}{2}BC\cdot OF+\frac{1}{2}AC\cdot OE=\frac{1}{2}(AB + BC + AC)\cdot OF$
已知$\triangle ABC$周长$AB + BC + AC = 30$，$OF = 3$。
则$S_{\triangle ABC}=\frac{1}{2}×30×3 = 45$。
综上，答案为：
(1)$OD = OE$，理由见上述步骤；
(2)$45$。