第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
同质训练 作出下列三角形的三条角平分线,并说说你的发现.


答案:
(画图步骤略,实际作答需按尺规作图规范作出三条角平分线)
发现:任意三角形的三条角平分线相交于一点,且该点在三角形内部。
发现:任意三角形的三条角平分线相交于一点,且该点在三角形内部。
例 在三角形中,从三角形的一个
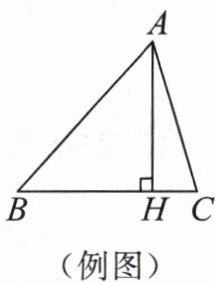
几何语言:如图,AH⊥BC,垂足为H,线段AH是△ABC的边BC上的高,必有∠
归纳小结:三角形的高必为
顶点
向它的对边所在直线画
垂线,顶点与垂足
之间的线段
叫作三角形的高线,简称三角形的高.几何语言:如图,AH⊥BC,垂足为H,线段AH是△ABC的边BC上的高,必有∠
AHB
= ∠AHC
= 90°.
归纳小结:三角形的高必为
线段
;三角形的高必过顶点垂直
于对边;三角形有三
条高.
答案:
顶点;对边所在直线画;垂足;线段;AHB;AHC;线段;垂直;三
同质训练 作出下列三角形的三条高,并思考下列问题:三角形的三条高交于一点吗?高与三角形的位置关系是怎样的?交点与三角形的位置关系又是怎样的呢?


答案:
答题
1. 作图:
锐角三角形:从三角形的一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段就是三角形的高。分别从三个顶点向对边作垂线,得到锐角三角形的三条高,这三条高相交于三角形内一点。
直角三角形:两条直角边互为对方的高,从直角顶点向斜边作垂线为第三条高,三条高相交于直角顶点。
钝角三角形:钝角两边上的高在三角形外部,从钝角的两个邻边顶点向对边作垂线在三角形内部,延长钝角所对的边,从钝角顶点向对边延长线作垂线,三条高所在直线相交于三角形外一点。
2. 回答问题:
三角形的三条高所在直线交于一点。
锐角三角形的三条高在三角形内部;直角三角形两条高在边上,一条高在三角形内部;钝角三角形两条高在三角形外部,一条高在三角形内部。
锐角三角形三条高的交点在三角形内部;直角三角形三条高的交点为直角顶点;钝角三角形三条高的交点在三角形外部。
1. 作图:
锐角三角形:从三角形的一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段就是三角形的高。分别从三个顶点向对边作垂线,得到锐角三角形的三条高,这三条高相交于三角形内一点。
直角三角形:两条直角边互为对方的高,从直角顶点向斜边作垂线为第三条高,三条高相交于直角顶点。
钝角三角形:钝角两边上的高在三角形外部,从钝角的两个邻边顶点向对边作垂线在三角形内部,延长钝角所对的边,从钝角顶点向对边延长线作垂线,三条高所在直线相交于三角形外一点。
2. 回答问题:
三角形的三条高所在直线交于一点。
锐角三角形的三条高在三角形内部;直角三角形两条高在边上,一条高在三角形内部;钝角三角形两条高在三角形外部,一条高在三角形内部。
锐角三角形三条高的交点在三角形内部;直角三角形三条高的交点为直角顶点;钝角三角形三条高的交点在三角形外部。
例 如图,在△ABC中,AD是边BC上的中线,AE是∠BAC的平分线,AF是边BC上的高.
(1)△ABD与△ADC之间的面积关系为
(2)若BC= 8cm,AF= 3cm,则△ABD的面积是
(3)若∠B= 42°,∠C= 70°,则∠FAE的度数是

(1)△ABD与△ADC之间的面积关系为
$S_{\triangle ABD}=S_{\triangle ADC}$
.(2)若BC= 8cm,AF= 3cm,则△ABD的面积是
6
$cm^2.$(3)若∠B= 42°,∠C= 70°,则∠FAE的度数是
$14^{\circ}$
.
答案:
(1)
因为$AD$是边$BC$上的中线,所以$BD = DC$,点$A$到$BC$的距离就是$\triangle ABD$与$\triangle ADC$的高,根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),可知$\triangle ABD$与$\triangle ADC$等底等高,所以$S_{\triangle ABD}=S_{\triangle ADC}$。
(2)
因为$AD$是$BC$边上的中线,$BC = 8cm$,所以$BD=\frac{1}{2}BC = 4cm$。
又因为$AF$是边$BC$上的高,所以$AF$为$\triangle ABD$中$BD$边上的高,$AF = 3cm$。
根据三角形面积公式$S=\frac{1}{2}ah$,可得$S_{\triangle ABD}=\frac{1}{2}× BD× AF=\frac{1}{2}×4×3 = 6cm^{2}$。
(3)
因为$AF$是边$BC$上的高,所以$\angle AFC = 90^{\circ}$。
在$\triangle ABC$中,$\angle B = 42^{\circ}$,$\angle C = 70^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle BAC=180^{\circ}-\angle B - \angle C=180^{\circ}-42^{\circ}-70^{\circ}=68^{\circ}$。
因为$AE$是$\angle BAC$的平分线,所以$\angle BAE=\frac{1}{2}\angle BAC = 34^{\circ}$。
在$\triangle ABF$中,$\angle B = 42^{\circ}$,$\angle AFC = 90^{\circ}$,所以$\angle BAF = 90^{\circ}-\angle B=90^{\circ}-42^{\circ}=48^{\circ}$。
则$\angle FAE=\angle BAF-\angle BAE = 48^{\circ}-34^{\circ}=14^{\circ}$。
综上,答案依次为:
(1)$S_{\triangle ABD}=S_{\triangle ADC}$;
(2)$6$;
(3)$14^{\circ}$。
(1)
因为$AD$是边$BC$上的中线,所以$BD = DC$,点$A$到$BC$的距离就是$\triangle ABD$与$\triangle ADC$的高,根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),可知$\triangle ABD$与$\triangle ADC$等底等高,所以$S_{\triangle ABD}=S_{\triangle ADC}$。
(2)
因为$AD$是$BC$边上的中线,$BC = 8cm$,所以$BD=\frac{1}{2}BC = 4cm$。
又因为$AF$是边$BC$上的高,所以$AF$为$\triangle ABD$中$BD$边上的高,$AF = 3cm$。
根据三角形面积公式$S=\frac{1}{2}ah$,可得$S_{\triangle ABD}=\frac{1}{2}× BD× AF=\frac{1}{2}×4×3 = 6cm^{2}$。
(3)
因为$AF$是边$BC$上的高,所以$\angle AFC = 90^{\circ}$。
在$\triangle ABC$中,$\angle B = 42^{\circ}$,$\angle C = 70^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle BAC=180^{\circ}-\angle B - \angle C=180^{\circ}-42^{\circ}-70^{\circ}=68^{\circ}$。
因为$AE$是$\angle BAC$的平分线,所以$\angle BAE=\frac{1}{2}\angle BAC = 34^{\circ}$。
在$\triangle ABF$中,$\angle B = 42^{\circ}$,$\angle AFC = 90^{\circ}$,所以$\angle BAF = 90^{\circ}-\angle B=90^{\circ}-42^{\circ}=48^{\circ}$。
则$\angle FAE=\angle BAF-\angle BAE = 48^{\circ}-34^{\circ}=14^{\circ}$。
综上,答案依次为:
(1)$S_{\triangle ABD}=S_{\triangle ADC}$;
(2)$6$;
(3)$14^{\circ}$。
同质训练 如图,在△ABC中,AD是边BC上的中线,AE是∠BAC的平分线,AF是边BC上的高.
(1)若AB= 10cm,AC= 4cm,则△ABD与△ACD的周长之差为
(2)若∠B= m°,∠C= n°,求∠FAE的度数.
(1)若AB= 10cm,AC= 4cm,则△ABD与△ACD的周长之差为
6
cm.(2)若∠B= m°,∠C= n°,求∠FAE的度数.
$\frac{|m - n|}{2}$°
答案:
(1)
∵AD是BC边上的中线,
∴BD=CD。
△ABD周长=AB+BD+AD,△ACD周长=AC+CD+AD。
周长差=(AB+BD+AD)-(AC+CD+AD)=AB-AC。
∵AB=10cm,AC=4cm,
∴10-4=6(cm)。
(2) 在△ABC中,∠BAC=180°-∠B-∠C=180°-m°-n°。
∵AE平分∠BAC,
∴∠CAE=∠BAC/2=(180°-m°-n°)/2=90°-(m+n)/2 °。
∵AF是BC边上的高,
∴∠AFC=90°,在Rt△AFC中,∠CAF=90°-∠C=90°-n°。
∴∠FAE=∠CAF-∠CAE=(90°-n°)-[90°-(m+n)/2 °]=(m-n)/2 °。
(1) 6
(2) $\frac{|m - n|}{2}$°
(1)
∵AD是BC边上的中线,
∴BD=CD。
△ABD周长=AB+BD+AD,△ACD周长=AC+CD+AD。
周长差=(AB+BD+AD)-(AC+CD+AD)=AB-AC。
∵AB=10cm,AC=4cm,
∴10-4=6(cm)。
(2) 在△ABC中,∠BAC=180°-∠B-∠C=180°-m°-n°。
∵AE平分∠BAC,
∴∠CAE=∠BAC/2=(180°-m°-n°)/2=90°-(m+n)/2 °。
∵AF是BC边上的高,
∴∠AFC=90°,在Rt△AFC中,∠CAF=90°-∠C=90°-n°。
∴∠FAE=∠CAF-∠CAE=(90°-n°)-[90°-(m+n)/2 °]=(m-n)/2 °。
(1) 6
(2) $\frac{|m - n|}{2}$°
查看更多完整答案,请扫码查看


