《2025年新课程示径学案作业设计八年级数学上册苏科版》

例 1 求下列各数的平方根.
(1)100；(2)625；(3)0.0081；(4)2；(5)81；(6)2.56；(7)$ \left|-2 \frac{1}{4}\right| $；(8)$ 10^{-2} $.
归纳小结：求一个数的平方根的运算叫作开平方.

答案：
(1)
解：因为$( \pm 10)^{2} = 100$，
所以$100$的平方根为$\pm 10$；
(2)
解：因为$( \pm 25)^{2} = 625$，
所以$625$的平方根为$\pm 25$；
(3)
解：因为$( \pm 0.09)^{2} = 0.0081$，
所以$0.0081$的平方根为$\pm 0.09$；
(4)
解：因为$( \pm \sqrt{2})^{2} = 2\approx(\pm1.414)^2$，
在精确度不高的情况下，可以说$2$的平方根约为$\pm 1.414$，
精确表示为$\pm \sqrt{2}$；
(5)
解：因为$( \pm 9)^{2} = 81$，
所以$81$的平方根为$\pm 9$；
(6)
解：因为$( \pm 1.6)^{2} = 2.56$，
所以$2.56$的平方根为$\pm 1.6$；
(7)
解：$\left| - 2\frac{1}{4} \right|=\frac{9}{4}$，
因为$( \pm \frac{3}{2})^{2} = \frac{9}{4}$，
所以$\left| - 2\frac{1}{4} \right|$的平方根为$\pm \frac{3}{2}$；
(8)
解：$10^{- 2}=\frac{1}{100}$，
因为$( \pm \frac{1}{10})^{2} = \frac{1}{100}=10^{-2}$，
所以$10^{- 2}$的平方根为$\pm \frac{1}{10}$，即$\pm 0.1$。

同质训练 1 求下列各数的平方根.
(1)0.01；(2)$ \frac{16}{25} $；(3)0；(4)10；(5)$ \left(-\frac{1}{3}\right)^{2} $.

答案：
(1)±0.1；
(2)±$\frac{4}{5}$；
(3)0；
(4)±$\sqrt{10}$；
(5)±$\frac{1}{3}$

同质训练 2 (1)64 的平方根是±8,$ 10^{2} $ 的平方根是±10,$ \frac{9}{25} $ 的平方根是±$\frac{3}{5}$,$ \sqrt{81} $ 的算术平方根是3.
(2)若 $ \sqrt{a}= 1.2 $,则 $ a= $1.44；若 $ \sqrt{m^{2}}= 4 $,则 $ m= $±4.
(3)若代数式 $ 2+x $ 有平方根,则 $ x $ 的取值范围是$x \geq - 2$.

答案：
(1)$\pm 8$，$\pm 10$，$\pm \frac{3}{5}$，$3$；
(2)$1.44$，$\pm 4$；
(3)$x \geq - 2$。

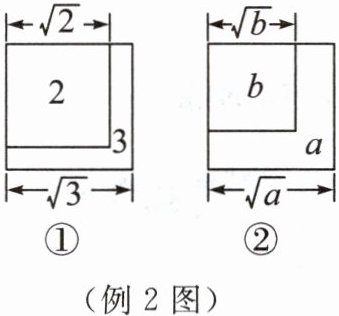
例 2 如图①,将面积为 2 的正方形纸片放置在面积为 3 的正方形纸片上.
(1)比较 $ \sqrt{2} $ 与 $ \sqrt{3} $ 的大小；
(2)已知 $ a＞b＞0 $,类似地,根据图②,比较 $ \sqrt{a} $ 与 $ \sqrt{b} $ 的大小.

答案：
(1)因为$2＜3$，根据正方形面积与边长的关系，面积为$2$的正方形边长为$\sqrt{2}$，面积为$3$的正方形边长为$\sqrt{3}$，且两个正方形边长都为正数，所以$\sqrt{2}＜\sqrt{3}$。
(2)因为$a ＞ b＞0$，根据正方形面积与边长的关系，大正方形面积为$a$，其边长为$\sqrt{a}$，小正方形面积为$b$，其边长为$\sqrt{b}$，且两个正方形边长都为正数，所以$\sqrt{a}＞\sqrt{b}$。

同质训练 3 求下列各式中的 $ x $.
(1)$ x^{2}= 16 $；(2)$ x^{2}= \frac{49}{25} $；(3)$ x^{2}= 2 $.

答案：
(1)
由 $x^{2} = 16$，根据平方根的定义，得 $x = \pm 4$。
(2)
由 $x^{2} = \frac{49}{25}$，根据平方根的定义，得 $x = \pm \frac{7}{5}$。
(3)
由 $x^{2} = 2$，根据平方根的定义，得 $x = \pm \sqrt{2}$。

同质训练 4 正数 $ a $ 的两个平方根分别是 $ x+1 $,$ 2x-1 $.求：
(1)$ x $ 的值；
(2)$ a $ 的值.

答案：
(1)因为正数$a$的两个平方根互为相反数，所以$x + 1 + 2x - 1 = 0$，$3x = 0$，解得$x = 0$。
(2)由
(1)知$x = 0$，则$x + 1 = 0 + 1 = 1$，所以$a = 1^2 = 1$。
(1)$x = 0$；
(2)$a = 1$