《2025年新课程示径学案作业设计八年级数学上册苏科版》

例 1 如图,在△ABC中,AB = AC,AD是边BC上的中线。求证：△ABD ≌ △ACD。

答案： 证明：
∵AD是边BC上的中线，
∴BD=CD。
在△ABD和△ACD中，
AB=AC（已知），
AD=AD（公共边），
BD=CD（已证），
∴△ABD≌△ACD（SSS）。

例 2 如图,AB = DE,BC = EF,AD = CF。求证：△ABC ≌ △DEF。

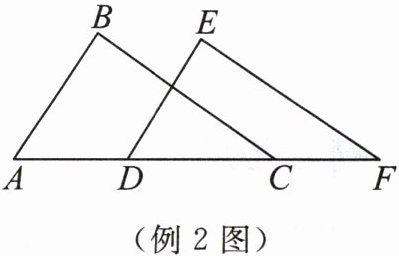
答案： 证明：
$\because AD = CF$，
$\therefore AD + DC = CF + DC$，
即$AC = DF$，
在$\bigtriangleup ABC$和$\bigtriangleup DEF$中，
$\begin{cases}AB = DE \\BC = EF \\AC = DF\end{cases}$
$\therefore \bigtriangleup ABC ≌ \bigtriangleup DEF(SSS)$。

例 1 用三根细木棒钉成一个三角形框架,它的形状会改变吗？为什么？用四根细木棒钉成的四边形框架呢？
归纳小结：三角形具有稳定性，四边形不具有稳定性。

答案： 三角形框架形状不会改变。因为三角形三边长度确定，根据边边边全等三角形判定定理，三角形的形状和大小唯一确定。
四边形框架形状会改变。因为四边形四边长度确定时，其内角可以改变，形状不唯一。
归纳小结：三角形具有稳定性，四边形不具有稳定性。

例 2 三角形的稳定性在生活中有广泛的应用,你能举出一些例子吗？

答案： 自行车车架、照相机三脚架、屋顶的三角形钢架、起重机的三角形吊臂。