《2025年新课程示径学案作业设计八年级数学上册苏科版》

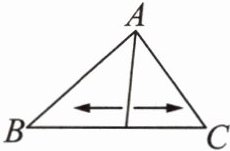
如图,橡皮筋的一端固定在△ABC的顶点A处,另一端在边BC上移动.在这个过程中,橡皮筋(线段)的位置不断变化.你认为其中有哪些位置是特殊的？

答案： 三角形的中线、角平分线、高

例 在三角形中,连接一个顶点与它对边中点的线段,叫作三角形的中线.
几何语言：如图,点D在BC上,BD= CD,线段AD是△ABC的中线,必有BD=CD= $\frac{1}{2}BC$.

归纳小结：三角形的中线必为线段；三角形的中线必平分对边；三角形有3条中线.

答案： 中点；BD；CD；线段；平分；3

同质训练 作出下列三角形的三条中线,并说说你的发现.

答案： 答题卡：
1. 作锐角三角形三条中线：
分别找到三角形三边的中点，然后用线段将顶点与对边中点相连，三条中线相交于三角形内一点。
2. 作直角三角形三条中线：
同样先找到三边中点，再连接顶点与对边中点，三条中线也相交于三角形内一点。
3. 作钝角三角形三条中线：
找到三边中点后连接顶点与对边中点，三条中线还是相交于三角形内一点。
发现：三角形的三条中线相交于一点。

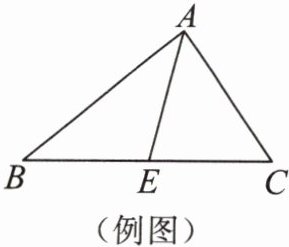
例 在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.
几何语言：如图,点E在BC上,∠BAE= ∠CAE,线段AE是△ABC的角平分线,必有∠BAE= ∠CAE= $\frac{1}{2}∠BAC$.

归纳小结：三角形的角平分线必为线段,而一个角的角平分线为一条射线；三角形的角平分线必过顶点平分三角形的一内角；三角形有三条角平分线.

答案： 对边；交点；线段；BAE；CAE；线段；射线；三