《2025年新课程示径学案作业设计八年级数学上册苏科版》

1. 判定两个三角形全等的方法:SSS（边边边写成文字也视为正确答案形式）,SAS,ASA,AAS.

答案： SSS（边边边写成文字也视为正确答案形式），SAS，ASA，AAS

2. 舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花棚遮住无法测量.工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他认为“两个直角三角形是全等的”.你同意他的结论吗?

答案： 同意。
设两个直角三角形分别为$\triangle ABC$和$\triangle A'B'C'$，
其中$\angle B$和$\angle B'$为直角。
假设未被遮住的直角边分别为$AB = A'B'$，斜边分别为$AC = A'C'$。
根据直角三角形全等的$HL$（Hypotenuse-Leg）判定定理：
如果两个直角三角形的斜边和一条直角边分别对应相等，
那么这两个直角三角形全等。
因此，$\triangle ABC \cong \triangle A'B'C'$（$HL$）。
所以两个直角三角形全等。

例1 我们知道,两个三角形满足“边边角”对应相等的条件,不能保证这两个三角形全等.那么在两个直角三角形中,当斜边和一条直角边分别相等,且满足“边边角”对应相等的条件时,这两个直角三角形能否全等呢?

答案： 答题卡：
可以全等。
设两个直角三角形分别为$\triangle ABC$和$\triangle A'B'C'$，其中$\angle C = \angle C' = 90°$，斜边$AB = A'B'$，一条直角边$AC = A'C'$。
根据HL（Hypotenuse-Leg）全等判定定理，如果两个直角三角形的一条直角边和斜边分别对应相等，则这两个直角三角形全等。
因此，$\triangle ABC \cong \triangle A'B'C'$（HL）。
所以，在两个直角三角形中，当斜边和一条直角边分别相等时，这两个直角三角形全等。

例2 如图,给定直角三角形 $ ABC $,简记为“$ Rt\triangle ABC $”.用直尺和圆规作 $ Rt\triangle A'B'C' $,使得 $ \angle C' = 90^{\circ},A'B' = AB,A'C' = AC $.这两个三角形全等吗?

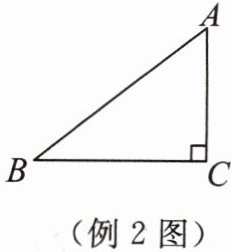
归纳小结:斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”).

答案： 这两个三角形全等；斜边和一条直角边分别相等的；斜边、直角边。