第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
例 把下列各数填入相应的集合内:$3\frac{1}{2}$,$\sqrt[3]{-8}$,$0$,$\sqrt{27}$,$\frac{\pi}{3}$,$0.5$,$3.14159$,$-0.020020002$,$0.12121121112…$(相邻的两个$2之间依次多一个1$)
(1)有理数:$\{ $
(2)无理数:$\{ $
(3)正实数:$\{ $
(4)负实数:$\{ $
归纳小结:(1)
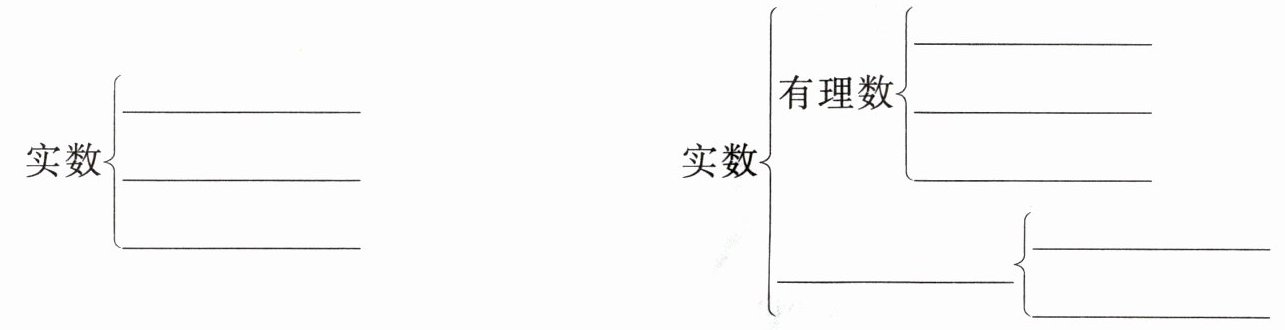
(2)实数可以这样分类:
$实数\begin{cases} &
$实数\begin{cases} 有理数\begin{cases}
(1)有理数:$\{ $
$3\frac{1}{2},\sqrt[3]{-8},0,0.5,3.14159,-0.020020002$
$\}$;(2)无理数:$\{ $
$\sqrt{27},\frac{\pi}{3},0.12121121112…$
$\}$;(3)正实数:$\{ $
$3\frac{1}{2},\sqrt{27},\frac{\pi}{3},0.5,3.14159,0.12121121112…$
$\}$;(4)负实数:$\{ $
$\sqrt[3]{-8},-0.020020002$
$\}$.归纳小结:(1)
有理数
和无理数
统称为实数.(2)实数可以这样分类:
$实数\begin{cases} &
正实数
\\ & 0
\\ & 负实数
\end{cases}$$实数\begin{cases} 有理数\begin{cases}
正有理数
\\ 0
\\ 负有理数
\end{cases} \\ 无理数\begin{cases} 正无理数
\\ 负无理数
\end{cases} \end{cases}$
答案:
(1)有理数:$\left\{3\frac{1}{2},\sqrt[3]{-8},0,0.5,3.14159,-0.020020002\right\}$;
(2)无理数:$\left\{\sqrt{27},\frac{\pi}{3},0.12121121112…\right\}$;
(3)正实数:$\left\{3\frac{1}{2},\sqrt{27},\frac{\pi}{3},0.5,3.14159,0.12121121112…\right\}$;
(4)负实数:$\left\{\sqrt[3]{-8},-0.020020002\right\}$;
归纳小结:
(1)有理数;无理数;
(2)
第一个图(按正负分):正实数;0;负实数;
第二个图(按定义分):有理数;无理数;正有理数;0;负有理数;正无理数;负无理数。
(1)有理数:$\left\{3\frac{1}{2},\sqrt[3]{-8},0,0.5,3.14159,-0.020020002\right\}$;
(2)无理数:$\left\{\sqrt{27},\frac{\pi}{3},0.12121121112…\right\}$;
(3)正实数:$\left\{3\frac{1}{2},\sqrt{27},\frac{\pi}{3},0.5,3.14159,0.12121121112…\right\}$;
(4)负实数:$\left\{\sqrt[3]{-8},-0.020020002\right\}$;
归纳小结:
(1)有理数;无理数;
(2)
第一个图(按正负分):正实数;0;负实数;
第二个图(按定义分):有理数;无理数;正有理数;0;负有理数;正无理数;负无理数。
例 1 如图,请在数轴上找到表示$\sqrt{2}和-\sqrt{3}$的点.

归纳小结:每个实数都可以用数轴上的一个点来表示,反之数轴上的每一个点都表示一个实数,

归纳小结:每个实数都可以用数轴上的一个点来表示,反之数轴上的每一个点都表示一个实数,
实数
与数轴上的点一一对应.
答案:
本题可利用勾股定理在数轴上找到表示$\sqrt{2}$和$-\sqrt{3}$的点。
1. 在数轴上找到表示$\sqrt{2}$的点
以数轴的原点$0$为直角顶点,作一个单位长度($1$个单位长度为数轴上$1$个小格的长度)的横向线段$OA$和$1$个单位长度的纵向线段$AB$,连接$OB$。
根据勾股定理,在直角三角形$OAB$中,$OA = 1$,$AB = 1$,则$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{1^{2} + 1^{2}}=\sqrt{2}$。
以原点$O$为圆心,$OB$长为半径画弧,交数轴正半轴于点$C$,点$C$表示的数就是$\sqrt{2}$。
2. 在数轴上找到表示$-\sqrt{3}$的点
以数轴的原点$0$为直角顶点,作$1$个单位长度的横向线段$OD$和$\sqrt{2}$个单位长度的纵向线段$DE$($\sqrt{2}$的长度可通过上述作$\sqrt{2}$的方法得到),连接$OE$。
根据勾股定理,在直角三角形$ODE$中,$OD = 1$,$DE=\sqrt{2}$,则$OE=\sqrt{OD^{2}+DE^{2}}=\sqrt{1^{2}+(\sqrt{2})^{2}}=\sqrt{3}$。
以原点$O$为圆心,$OE$长为半径画弧,交数轴负半轴于点$F$,点$F$表示的数就是$-\sqrt{3}$。
归纳小结
每个实数都可以用数轴上的一个点来表示,反之数轴上的每一个点都表示一个实数,实数与数轴上的点一一对应。
故答案依次为:在数轴上按上述步骤作出表示$\sqrt{2}$和$-\sqrt{3}$的点(具体作图过程略);实数。
1. 在数轴上找到表示$\sqrt{2}$的点
以数轴的原点$0$为直角顶点,作一个单位长度($1$个单位长度为数轴上$1$个小格的长度)的横向线段$OA$和$1$个单位长度的纵向线段$AB$,连接$OB$。
根据勾股定理,在直角三角形$OAB$中,$OA = 1$,$AB = 1$,则$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{1^{2} + 1^{2}}=\sqrt{2}$。
以原点$O$为圆心,$OB$长为半径画弧,交数轴正半轴于点$C$,点$C$表示的数就是$\sqrt{2}$。
2. 在数轴上找到表示$-\sqrt{3}$的点
以数轴的原点$0$为直角顶点,作$1$个单位长度的横向线段$OD$和$\sqrt{2}$个单位长度的纵向线段$DE$($\sqrt{2}$的长度可通过上述作$\sqrt{2}$的方法得到),连接$OE$。
根据勾股定理,在直角三角形$ODE$中,$OD = 1$,$DE=\sqrt{2}$,则$OE=\sqrt{OD^{2}+DE^{2}}=\sqrt{1^{2}+(\sqrt{2})^{2}}=\sqrt{3}$。
以原点$O$为圆心,$OE$长为半径画弧,交数轴负半轴于点$F$,点$F$表示的数就是$-\sqrt{3}$。
归纳小结
每个实数都可以用数轴上的一个点来表示,反之数轴上的每一个点都表示一个实数,实数与数轴上的点一一对应。
故答案依次为:在数轴上按上述步骤作出表示$\sqrt{2}$和$-\sqrt{3}$的点(具体作图过程略);实数。
同质训练 1 找出下列各数中的无理数,并把它们表示在数轴上:$\sqrt{\frac{9}{16}}$,$-\frac{22}{7}$,$\sqrt{3}$,$\sqrt[3]{8}$,$-\sqrt{2}$,$\pi + 3$.
答案:
无理数:$\sqrt{3}$,$-\sqrt{2}$,$\pi + 3$。
数轴表示:(注:此处因无法直接画图,实际作答时需在数轴上分别标出表示$\sqrt{3}$(约1.732)、$-\sqrt{2}$(约-1.414)、$\pi + 3$(约6.1416)的点,具体画法为利用勾股定理构造直角三角形得到对应无理数的长度,再在数轴上截取相应位置。)
数轴表示:(注:此处因无法直接画图,实际作答时需在数轴上分别标出表示$\sqrt{3}$(约1.732)、$-\sqrt{2}$(约-1.414)、$\pi + 3$(约6.1416)的点,具体画法为利用勾股定理构造直角三角形得到对应无理数的长度,再在数轴上截取相应位置。)
查看更多完整答案,请扫码查看


