第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 新趋势 算理理解 看图补充等量关系式,再列出方程。
(1)小可和小乐x分钟后相遇。
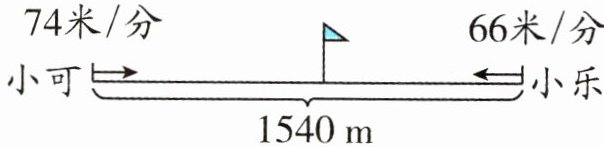
列方程:
(2)小阳和小月已经走了8分钟了。
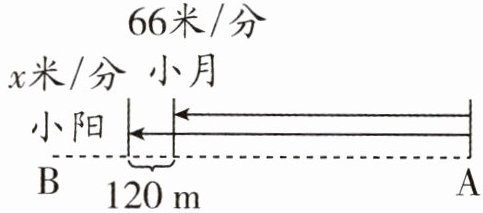
列方程:
(1)小可和小乐x分钟后相遇。

小可走的路程
+小乐走的路程
= 总路程列方程:
74x+66x=1540
。(2)小阳和小月已经走了8分钟了。

小阳走的路程
-小月走的路程
= 120m列方程:
8x-66×8=120
。
答案:
1.
(1)小可走的路程 小乐走的路程 74x+66x=1540
(2)小阳走的路程 小月走的路程 8x-66×8=120
(1)小可走的路程 小乐走的路程 74x+66x=1540
(2)小阳走的路程 小月走的路程 8x-66×8=120
2. “冰丝带”国家速滑馆是北京冬奥会的标志性建筑,拥有目前亚洲最大的冰面。李叔叔和王叔叔相约在“元旦”期间去参观国家速滑馆,他们分别从相距112km的两地同时出发,相向而行,王叔叔骑摩托车每小时行54km。
(1)如果李叔叔骑自行车每小时行16km,那么两人几小时后相遇?
(2)如果他们经过1.4小时相遇,那么李叔叔骑自行车每小时行多少千米?(列方程解答)
(1)如果李叔叔骑自行车每小时行16km,那么两人几小时后相遇?
(2)如果他们经过1.4小时相遇,那么李叔叔骑自行车每小时行多少千米?(列方程解答)
答案:
2.
(1)解:设两人x小时后相遇。(54+16)x=112 x=1.6 答:两人1.6小时后相遇。
(2)解:设李叔叔骑自行车每小时行x km。(54+x)×1.4=112 x=26 答:李叔叔骑自行车每小时行26 km。
(1)解:设两人x小时后相遇。(54+16)x=112 x=1.6 答:两人1.6小时后相遇。
(2)解:设李叔叔骑自行车每小时行x km。(54+x)×1.4=112 x=26 答:李叔叔骑自行车每小时行26 km。
3. 一条公路长530m,两辆清雪车同时从公路的两端往中间清理积雪。甲车的清理速度是乙车的1.5倍,3小时后这条公路只剩50m没有清理干净。乙车每小时清理积雪多少米?(列方程解答)
答案:
3.解:设乙车每小时清理积雪x m,则甲车每小时清理积雪1.5x m。 (1.5x+x)×3=530-50 x=64 答:乙车每小时清理积雪64 m。
4. A、B两地相距180km,甲、乙两艘邮轮同时从两地出发,相向而行。甲邮轮每小时行驶52km,1.5小时后两邮轮相距21km,乙邮轮每小时行驶多少千米?(列方程解答)
答案:
4.解:设乙邮轮每小时行驶x千米。(52+x)×1.5=180-21 x=54 (52+x)×1.5=180+21 x=82 答:乙邮轮每小时行驶54千米或82千米。
5. 甲车的速度是乙车速度的2.2倍,下午3时两车分别从A地和B地相对开出,0.6小时后在离中点18km处相遇。两车相遇时各行驶了多少千米?(列方程解答)
答案:
5.解:设乙车每小时行驶x km,则甲车每小时行驶2.2x km。 0.6×(2.2x-x)=18×2 x=50 2.2x=110 甲车:110×0.6=66(km) 乙车:50×0.6=30(km) 答:两车相遇时甲车行驶了66 km,乙车行驶了30 km。 提示:甲、乙两车在离中点18 km处相遇,说明相遇时甲车比乙车多行驶了2×18=36(km)。
6. (选做题)两辆运送物资的车分别从两地同时相向而行,甲车的速度是60km/h,乙车的速度是40km/h,行驶一段时间后,甲车距离全程中点15km,乙车距离全程中点35km,两车从出发到相遇需要多少小时?(列方程解答)
答案:
6.情况一:两车都没有超过全程中点。解:设经过y小时后,甲车距离全程中点15 km,乙车距离全程中点35 km。 60y+15=40y+35 60y-40y=35-15 20y=20 y=20÷20 y=1 (60×1+15)×2÷(60+40)=(60+15)×2÷100=75×2÷100=1.5(小时) 情况二:甲车超过全程中点15 km,乙车未到全程中点,且离全程中点还有35 km。解:设经过x小时后,甲车超过全程中点且距离全程中点15 km,乙车未到全程中点,且距离全程中点35 km。 60x-15=40x+35 60x-40x=35+15 20x=50 x=50÷20 x=2.5 (60×2.5-15)×2÷(60+40)=(150-15)×2÷(60+40)=135×2÷100=2.7(小时) 答:两车从出发到相遇需要1.5小时或2.7小时。 提示:根据题意“行驶一段时间,甲车距离全程中点15 km,乙车距离全程中点35 km”可知,行驶一段时间后,可以分两种情况:
(1)两车都没有超过全程中点,甲车离全程中点还有15 km,乙车离全程中点还有35 km,此时可列等量关系式:甲车的速度×行驶时间+15=乙车的速度×行驶时间+35;
(2)因为甲车的速度大于乙车的速度,所以还有一种情况是甲车此时超过了全程中点15 km,乙车未到全程中点,且离全程中点还有35 km,此时可列等量关系式:甲车的速度×行驶时间-15=乙车的速度×行驶时间+35。根据两种情况先求出行驶时间,进而求出两车从出发到相遇需要的时间。
(1)两车都没有超过全程中点,甲车离全程中点还有15 km,乙车离全程中点还有35 km,此时可列等量关系式:甲车的速度×行驶时间+15=乙车的速度×行驶时间+35;
(2)因为甲车的速度大于乙车的速度,所以还有一种情况是甲车此时超过了全程中点15 km,乙车未到全程中点,且离全程中点还有35 km,此时可列等量关系式:甲车的速度×行驶时间-15=乙车的速度×行驶时间+35。根据两种情况先求出行驶时间,进而求出两车从出发到相遇需要的时间。
查看更多完整答案,请扫码查看


