第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 如图,点A,B,C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,给出下列说法:①MN= CH;②MH= $\frac{1}{2}(AH-BH)$;③MN= $\frac{1}{2}(AC+BH)$;④HN= $\frac{1}{2}(CH+BH)$.其中正确的是(
B
)
答案:
B 提示:因为 H 为 AC 的中点,M 为 AB 的中点,N 为 BC 的中点,所以 $ AH=CH=\frac{1}{2}AC $,$ AM=BM=\frac{1}{2}AB $,$ BN=CN=\frac{1}{2}BC $,所以 $ MN=BM+BN=\frac{1}{2}(AB+BC)=\frac{1}{2}AC=CH $,故①正确,③错误;因为 $ \frac{1}{2}(AH - BH)=\frac{1}{2}(AB - BH - BH)=BM - BH=MH $,故②正确;因为 $ \frac{1}{2}(CH + BH)=\frac{1}{2}(BC + BH + BH)=BN + BH=HN $,故④正确.
2. 如图,分别过直线AB上的点C和点D作射线CF,DE,∠BCF= 60°,∠EDB= 90°,射线DG从DE开始绕着点D以6°/s的速度按顺时针方向旋转,射线CH从CF开始绕着点C以1°/s的速度按顺时针方向旋转.在射线DG旋转一周的过程中,当射线DG,CH所在的直线互相垂直时,旋转时间t=
12 或 48
s.
答案:
12 或 48 提示:由题可知,射线 DG 旋转一周所需的时间为 $ \frac{360}{6}=60(s) $,则射线 CH 在此时间内旋转了 $ 60^{\circ} $.设射线 DG 旋转的时间为 t s 时,直线 DG⊥CH 于点 P,分情况讨论:如图 1,当射线 DG 在$ \angle EDB $内部,即 $ 0<t<15 $时,易知$ \angle CDP=\angle GDB=\angle EDB - \angle EDG=90^{\circ}-6t^{\circ} $,$ \angle DCP=\angle BCF+\angle FCH=60^{\circ}+t^{\circ} $,因为 DG⊥CH,所以$ \angle CPD=90^{\circ} $,所以$ \angle CDP+\angle DCP=90^{\circ} $,即$ (90 - 6t)^{\circ}+(60 + t)^{\circ}=90^{\circ} $,解得 t = 12.当射线 DG 在$ \angle EDB $外部且在直线 AB 上方,即 $ 45<t<60 $时,易知$ \angle GDE=360^{\circ}-6t^{\circ} $,$ \angle BCH=\angle BCF+\angle FCH=60^{\circ}+t^{\circ} $,所以$ \angle CDP=90^{\circ}-\angle GDE=90^{\circ}-(360 - 6t)^{\circ}=(6t - 270)^{\circ} $,$ \angle DCP=180^{\circ}-\angle BCH=180^{\circ}-(60 + t)^{\circ}=(120 - t)^{\circ} $.同理,$ \angle CDP+\angle DCP=90^{\circ} $,即$ (6t - 270)^{\circ}+(120 - t)^{\circ}=90^{\circ} $,解得 t = 48.(当射线 DG 在$ \angle EDB $外部且在直线 AB 下方,即 $ 15<t<45 $时,易知直线 DG 与直线 CH 不垂直)
3. 【探究】一个平面被n条直线分割,最多可以分成多少部分?

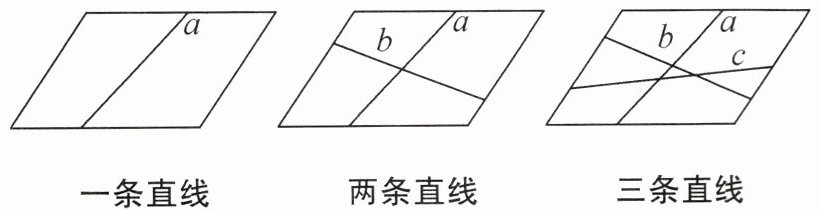
|直线条数|新直线被分成的份数|原平面被分成的份数|增加的平面份数|新平面被分成的份数|
|1|1|1|1|A(1)= 2|
|2|2|A(1)= 2|2|A(2)= 4|
|3|3|A(2)= 4|3|A(3)= 7|
|...|...|...|...|...|
|n|n|A(n-1)|n|A(n)|
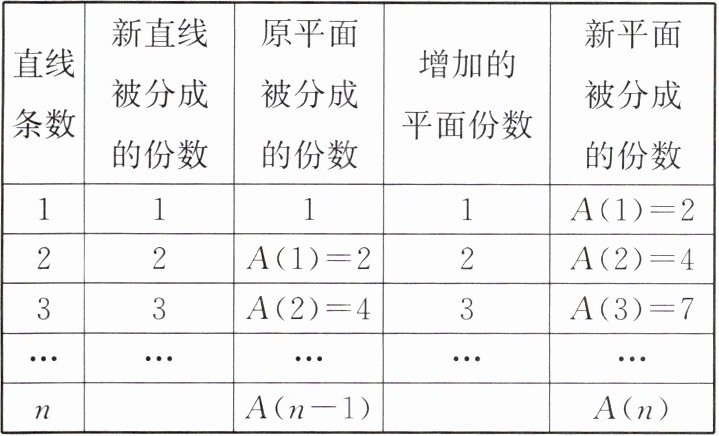
(1)填空:A(4)= ______.
(2)计算A(2)-A(1),A(3)-A(2),A(4)-A(3),…,A(n)-A(n-1),这(n-1)组差,再把这(n-1)组差相加可得A(n)-A(1)= ______,A(n)= ______.(用含n的式子表示)
【延伸】我们已知一条直线(一维)被n个点分割,最多可以分成n+1部分,即一维的分割数是n的一次多项式.经过证明,我们了解到二维的最多分割数是n的二次多项式,三维的最多分割数是n的三次多项式.我们解决一个平面(二维)被n条直线分割,最多可以分成多少部分的问题就有了新的办法.
(3)令这个二维分割数为$A(n)= kn^2+pn+q,$代入A(1)= 2,A(2)= 4,A(3)= 7,得A(n)= ______.(用含n的式子表示)
【类比】一个空间(用球体表示)被n个平面分割.(给出的图例如下)
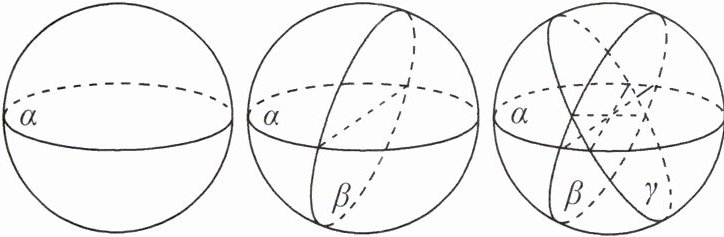
(4)请用以上两种方法分别得出三维分割数B(n).(用含n的式子表示)
(1)填空:A(4)=
(2)计算A(2)-A(1),A(3)-A(2),A(4)-A(3),…,A(n)-A(n-1),这(n-1)组差,再把这(n-1)组差相加可得A(n)-A(1)=
(3)令这个二维分割数为$A(n)= kn^2+pn+q,$代入A(1)= 2,A(2)= 4,A(3)= 7,得A(n)=
(4)请用以上两种方法分别得出三维分割数B(n).(用含n的式子表示)
方法一:1个平面把一个空间分成2部分,2个平面最多把一个空间分成4部分,3个平面最多把一个空间分成8部分,4个平面最多把一个空间分成15部分……所以B(2)-B(1)=4 - 2=2=1 + 1,B(3)-B(2)=8 - 4=4=1 + 1+2,B(4)-B(3)=15 - 8=7=1 + 1+2+3,…,以此类推,B(n)-B(n - 1)=1 + 1+2+3+…+(n - 1)=$\frac{1}{2}n(n - 1)+1$。一般地,有B(k)-B(k - 1)-1=$\frac{1}{2}k(k - 1)=\frac{1}{6}k(k - 1)[(k + 1)-(k - 2)]=\frac{1}{6}(k + 1)k(k - 1)-\frac{1}{6}k(k - 1)(k - 2)$,k = 2,3,…,n时均成立。所以[B(n)-B(n - 1)-1]+[B(n - 1)-B(n - 2)-1]+…+[B(3)-B(2)-1]+[B(2)-B(1)-1]=$[\frac{1}{6}(n + 1)n(n - 1)-\frac{1}{6}n(n - 1)(n - 2)]+[\frac{1}{6}n(n - 1)(n - 2)-\frac{1}{6}(n - 1)(n - 2)(n - 3)]+\cdots +(\frac{1}{6}× 4× 3× 2-\frac{1}{6}× 3× 2× 1)+(\frac{1}{6}× 3× 2× 1-\frac{1}{6}× 2× 1× 0)=\frac{1}{6}(n + 1)n(n - 1)$,即B(n)-B(1)-(n - 1)=$\frac{1}{6}(n + 1)n(n - 1)$,所以B(n)=$\frac{1}{6}(n + 1)n(n - 1)+B(1)+n - 1=\frac{1}{6}(n + 1)n(n - 1)+n + 1=\frac{1}{6}n^{3}+\frac{5}{6}n + 1$。
方法二:设B(n)=$an^{3}+bn^{2}+cn+d$,把B(1)=2,B(2)=4,B(3)=8,B(4)=15代入B(n)=$an^{3}+bn^{2}+cn+d$,得$\begin{cases}a + b + c + d = 2 \\ 8a + 4b + 2c + d = 4 \\ 27a + 9b + 3c + d = 8 \\ 64a + 16b + 4c + d = 15\end{cases}$解得$\begin{cases}a = \frac{1}{6} \\ b = 0 \\ c = \frac{5}{6} \\ d = 1\end{cases}$所以B(n)=$\frac{1}{6}n^{3}+\frac{5}{6}n + 1$。


|直线条数|新直线被分成的份数|原平面被分成的份数|增加的平面份数|新平面被分成的份数|
|1|1|1|1|A(1)= 2|
|2|2|A(1)= 2|2|A(2)= 4|
|3|3|A(2)= 4|3|A(3)= 7|
|...|...|...|...|...|
|n|n|A(n-1)|n|A(n)|

(1)填空:A(4)= ______.
(2)计算A(2)-A(1),A(3)-A(2),A(4)-A(3),…,A(n)-A(n-1),这(n-1)组差,再把这(n-1)组差相加可得A(n)-A(1)= ______,A(n)= ______.(用含n的式子表示)
【延伸】我们已知一条直线(一维)被n个点分割,最多可以分成n+1部分,即一维的分割数是n的一次多项式.经过证明,我们了解到二维的最多分割数是n的二次多项式,三维的最多分割数是n的三次多项式.我们解决一个平面(二维)被n条直线分割,最多可以分成多少部分的问题就有了新的办法.
(3)令这个二维分割数为$A(n)= kn^2+pn+q,$代入A(1)= 2,A(2)= 4,A(3)= 7,得A(n)= ______.(用含n的式子表示)
【类比】一个空间(用球体表示)被n个平面分割.(给出的图例如下)

(4)请用以上两种方法分别得出三维分割数B(n).(用含n的式子表示)
(1)填空:A(4)=
11
.(2)计算A(2)-A(1),A(3)-A(2),A(4)-A(3),…,A(n)-A(n-1),这(n-1)组差,再把这(n-1)组差相加可得A(n)-A(1)=
$\frac{1}{2}n^{2}+\frac{1}{2}n - 1$
,A(n)=$\frac{1}{2}n^{2}+\frac{1}{2}n + 1$
.(用含n的式子表示)(3)令这个二维分割数为$A(n)= kn^2+pn+q,$代入A(1)= 2,A(2)= 4,A(3)= 7,得A(n)=
$\frac{1}{2}n^{2}+\frac{1}{2}n + 1$
.(用含n的式子表示)(4)请用以上两种方法分别得出三维分割数B(n).(用含n的式子表示)
方法一:1个平面把一个空间分成2部分,2个平面最多把一个空间分成4部分,3个平面最多把一个空间分成8部分,4个平面最多把一个空间分成15部分……所以B(2)-B(1)=4 - 2=2=1 + 1,B(3)-B(2)=8 - 4=4=1 + 1+2,B(4)-B(3)=15 - 8=7=1 + 1+2+3,…,以此类推,B(n)-B(n - 1)=1 + 1+2+3+…+(n - 1)=$\frac{1}{2}n(n - 1)+1$。一般地,有B(k)-B(k - 1)-1=$\frac{1}{2}k(k - 1)=\frac{1}{6}k(k - 1)[(k + 1)-(k - 2)]=\frac{1}{6}(k + 1)k(k - 1)-\frac{1}{6}k(k - 1)(k - 2)$,k = 2,3,…,n时均成立。所以[B(n)-B(n - 1)-1]+[B(n - 1)-B(n - 2)-1]+…+[B(3)-B(2)-1]+[B(2)-B(1)-1]=$[\frac{1}{6}(n + 1)n(n - 1)-\frac{1}{6}n(n - 1)(n - 2)]+[\frac{1}{6}n(n - 1)(n - 2)-\frac{1}{6}(n - 1)(n - 2)(n - 3)]+\cdots +(\frac{1}{6}× 4× 3× 2-\frac{1}{6}× 3× 2× 1)+(\frac{1}{6}× 3× 2× 1-\frac{1}{6}× 2× 1× 0)=\frac{1}{6}(n + 1)n(n - 1)$,即B(n)-B(1)-(n - 1)=$\frac{1}{6}(n + 1)n(n - 1)$,所以B(n)=$\frac{1}{6}(n + 1)n(n - 1)+B(1)+n - 1=\frac{1}{6}(n + 1)n(n - 1)+n + 1=\frac{1}{6}n^{3}+\frac{5}{6}n + 1$。
方法二:设B(n)=$an^{3}+bn^{2}+cn+d$,把B(1)=2,B(2)=4,B(3)=8,B(4)=15代入B(n)=$an^{3}+bn^{2}+cn+d$,得$\begin{cases}a + b + c + d = 2 \\ 8a + 4b + 2c + d = 4 \\ 27a + 9b + 3c + d = 8 \\ 64a + 16b + 4c + d = 15\end{cases}$解得$\begin{cases}a = \frac{1}{6} \\ b = 0 \\ c = \frac{5}{6} \\ d = 1\end{cases}$所以B(n)=$\frac{1}{6}n^{3}+\frac{5}{6}n + 1$。
答案:
(1) 11
(2)$ \frac{1}{2}n^{2}+\frac{1}{2}n - 1 $$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $ 提示:由题中规律可知,A
(2)-A
(1)=2,A
(3)-A
(2)=3,A
(4)-A
(3)=4,…,A(n)-A(n - 1)=n,将这(n - 1)组差相加,得 A
(2)-A
(1)+A
(3)-A
(2)+A
(4)-A
(3)+…+A(n)-A(n - 1)=2+3+4+…+n,即$ A(n)-A(1)=2+3+4+\cdots +n=\frac{(n + 2)(n - 1)}{2}=\frac{1}{2}(n^{2}+n - 2)=\frac{1}{2}n^{2}+\frac{1}{2}n - 1 $,所以 A(n)-2=$ \frac{1}{2}n^{2}+\frac{1}{2}n - 1 $,所以 A(n)=$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $.
(3)$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $ 提示:把 A
(1)=2,A
(2)=4,A
(3)=7 分别代入 A(n)=$ kn^{2}+pn+q $,得$ \begin{cases} k + p + q = 2 \\ 4k + 2p + q = 4 \\ 9k + 3p + q = 7 \end{cases} $解得$ \begin{cases} k = \frac{1}{2} \\ p = \frac{1}{2} \\ q = 1 \end{cases} $所以 A(n)=$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $.
(4)方法一:1 个平面把一个空间分成 2 部分,2 个平面最多把一个空间分成 4 部分,3 个平面最多把一个空间分成 8 部分,4 个平面最多把一个空间分成 15 部分……所以 B
(2)-B
(1)=4 - 2=2=1 + 1,B
(3)-B
(2)=8 - 4=4=1 + 1+2,B
(4)-B
(3)=15 - 8=7=1 + 1+2+3,…,以此类推,B(n)-B(n - 1)=1 + 1+2+3+…+(n - 1)=$ \frac{1}{2}n(n - 1)+1 $.一般地,有 B(k)-B(k - 1)-1=$ \frac{1}{2}k(k - 1)=\frac{1}{6}k(k - 1)[(k + 1)-(k - 2)]=\frac{1}{6}(k + 1)k(k - 1)-\frac{1}{6}k(k - 1)(k - 2) $,k = 2,3,…,n 时均成立.所以[B(n)-B(n - 1)-1]+[B(n - 1)-B(n - 2)-1]+…+[B
(3)-B
(2)-1]+[B
(2)-B
(1)-1]=$ [\frac{1}{6}(n + 1)n(n - 1)-\frac{1}{6}n(n - 1)(n - 2)]+[\frac{1}{6}n(n - 1)(n - 2)-\frac{1}{6}(n - 1)(n - 2)(n - 3)]+\cdots +(\frac{1}{6}× 4× 3× 2-\frac{1}{6}× 3× 2× 1)+(\frac{1}{6}× 3× 2× 1-\frac{1}{6}× 2× 1× 0)=\frac{1}{6}(n + 1)n(n - 1) $,即 B(n)-B
(1)-(n - 1)=$ \frac{1}{6}(n + 1)n(n - 1) $,所以 B(n)=$ \frac{1}{6}(n + 1)n(n - 1)+B(1)+n - 1=\frac{1}{6}(n + 1)n(n - 1)+n + 1=\frac{1}{6}n^{3}+\frac{5}{6}n + 1 $.方法二:设 B(n)=$ an^{3}+bn^{2}+cn+d $,把 B
(1)=2,B
(2)=4,B
(3)=8,B
(4)=15 代入 B(n)=$ an^{3}+bn^{2}+cn+d $,得$ \begin{cases} a + b + c + d = 2 \\ 8a + 4b + 2c + d = 4 \\ 27a + 9b + 3c + d = 8 \\ 64a + 16b + 4c + d = 15 \end{cases} $解得$ \begin{cases} a = \frac{1}{6} \\ b = 0 \\ c = \frac{5}{6} \\ d = 1 \end{cases} $所以 B(n)=$ \frac{1}{6}n^{3}+\frac{5}{6}n + 1 $.
(1) 11
(2)$ \frac{1}{2}n^{2}+\frac{1}{2}n - 1 $$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $ 提示:由题中规律可知,A
(2)-A
(1)=2,A
(3)-A
(2)=3,A
(4)-A
(3)=4,…,A(n)-A(n - 1)=n,将这(n - 1)组差相加,得 A
(2)-A
(1)+A
(3)-A
(2)+A
(4)-A
(3)+…+A(n)-A(n - 1)=2+3+4+…+n,即$ A(n)-A(1)=2+3+4+\cdots +n=\frac{(n + 2)(n - 1)}{2}=\frac{1}{2}(n^{2}+n - 2)=\frac{1}{2}n^{2}+\frac{1}{2}n - 1 $,所以 A(n)-2=$ \frac{1}{2}n^{2}+\frac{1}{2}n - 1 $,所以 A(n)=$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $.
(3)$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $ 提示:把 A
(1)=2,A
(2)=4,A
(3)=7 分别代入 A(n)=$ kn^{2}+pn+q $,得$ \begin{cases} k + p + q = 2 \\ 4k + 2p + q = 4 \\ 9k + 3p + q = 7 \end{cases} $解得$ \begin{cases} k = \frac{1}{2} \\ p = \frac{1}{2} \\ q = 1 \end{cases} $所以 A(n)=$ \frac{1}{2}n^{2}+\frac{1}{2}n + 1 $.
(4)方法一:1 个平面把一个空间分成 2 部分,2 个平面最多把一个空间分成 4 部分,3 个平面最多把一个空间分成 8 部分,4 个平面最多把一个空间分成 15 部分……所以 B
(2)-B
(1)=4 - 2=2=1 + 1,B
(3)-B
(2)=8 - 4=4=1 + 1+2,B
(4)-B
(3)=15 - 8=7=1 + 1+2+3,…,以此类推,B(n)-B(n - 1)=1 + 1+2+3+…+(n - 1)=$ \frac{1}{2}n(n - 1)+1 $.一般地,有 B(k)-B(k - 1)-1=$ \frac{1}{2}k(k - 1)=\frac{1}{6}k(k - 1)[(k + 1)-(k - 2)]=\frac{1}{6}(k + 1)k(k - 1)-\frac{1}{6}k(k - 1)(k - 2) $,k = 2,3,…,n 时均成立.所以[B(n)-B(n - 1)-1]+[B(n - 1)-B(n - 2)-1]+…+[B
(3)-B
(2)-1]+[B
(2)-B
(1)-1]=$ [\frac{1}{6}(n + 1)n(n - 1)-\frac{1}{6}n(n - 1)(n - 2)]+[\frac{1}{6}n(n - 1)(n - 2)-\frac{1}{6}(n - 1)(n - 2)(n - 3)]+\cdots +(\frac{1}{6}× 4× 3× 2-\frac{1}{6}× 3× 2× 1)+(\frac{1}{6}× 3× 2× 1-\frac{1}{6}× 2× 1× 0)=\frac{1}{6}(n + 1)n(n - 1) $,即 B(n)-B
(1)-(n - 1)=$ \frac{1}{6}(n + 1)n(n - 1) $,所以 B(n)=$ \frac{1}{6}(n + 1)n(n - 1)+B(1)+n - 1=\frac{1}{6}(n + 1)n(n - 1)+n + 1=\frac{1}{6}n^{3}+\frac{5}{6}n + 1 $.方法二:设 B(n)=$ an^{3}+bn^{2}+cn+d $,把 B
(1)=2,B
(2)=4,B
(3)=8,B
(4)=15 代入 B(n)=$ an^{3}+bn^{2}+cn+d $,得$ \begin{cases} a + b + c + d = 2 \\ 8a + 4b + 2c + d = 4 \\ 27a + 9b + 3c + d = 8 \\ 64a + 16b + 4c + d = 15 \end{cases} $解得$ \begin{cases} a = \frac{1}{6} \\ b = 0 \\ c = \frac{5}{6} \\ d = 1 \end{cases} $所以 B(n)=$ \frac{1}{6}n^{3}+\frac{5}{6}n + 1 $.
查看更多完整答案,请扫码查看


