《2025年小题狂做七年级数学上册苏科版巅峰版》

10. 如图,下列图形是由一些小正方形和实心圆按一定规律排列而成,按此规律排列下去,记图n中实心圆的个数为K_{n}.
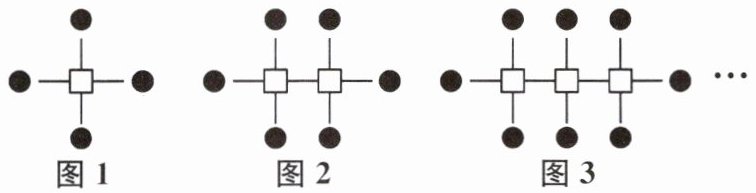
(1)K_{100}=202,K_{n}=2n+2(用含n的代数式表示).
(2)我们用“☆”定义一种新运算：对于任意有理数a和正整数n,规定$a☆n= \frac{a-K_{n}+|a+K_{n}|}{2}.$
例如：$(-3)☆2= \frac{-3-K_{2}+|-3+K_{2}|}{2}= \frac{-3-6+|-3+6|}{2}= \frac{-9+3}{2}= -3.$
①计算：(-26.6)☆10的值；
②比较3☆n与(-3)☆n的大小.
…

(2)解:①(-26.6)☆10=(-26.6-K₁₀+|-26.6+K₁₀|)/2=(-26.6-22+|-26.6+22|)/2=-22.
②因为n是正整数,所以Kₙ=2n+2≥4,所以3☆n=(3-Kₙ+|3+Kₙ|)/2=(3-Kₙ+3+Kₙ)/2=3,(-3)☆n=(-3-Kₙ+|-3+Kₙ|)/2=(-3-Kₙ-3+Kₙ)/2=-3.所以3☆n＞(-3)☆n.

答案：
(1)202 2n+2
(2)解:①(-26.6)☆10=(-26.6-K₁₀+|-26.6+K₁₀|)/2=(-26.6-22+|-26.6+22|)/2=-22.
②因为n是正整数,所以Kₙ=2n+2≥4,所以3☆n=(3-Kₙ+|3+Kₙ|)/2=(3-Kₙ+3+Kₙ)/2=3,(-3)☆n=(-3-Kₙ+|-3+Kₙ|)/2=(-3-Kₙ-3+Kₙ)/2=-3.所以3☆n＞(-3)☆n.

11. 如果两个多项式的和为单项式,则称它们互为“孪生多项式”,这个单项式称为它们的“孪生式”.如多项式$M= 3x^{2}-4x+7与多项式N= -3x^{2}+4x-4$,$M+N= 3$,3是单项式,则M与N互为“孪生多项式”,它们的“孪生式”为3；又如多项式$P= 3x^{2}-3x+7与多项式Q= -3x^{2}+4x-4$,$P+Q= x+3$,$x+3$不是单项式,则P与Q不是“孪生多项式”.
(1)分别判断下列两组多项式是否互为“孪生多项式”.如果是,写出它们的“孪生式”；如果不是,请说明理由.
①$5x^{2}-3与5x^{2}+2$；
②$ab^{2}+a^{2}b+1与-2a^{2}b-ab^{2}-1$.
(2)若$A= 2x^{2}-2x+3m与B= nx^{2}+4x+1$互为“孪生多项式”,m和n为常数,求$m+n$的值.
(3)在第(2)问的条件下,若多项式$C= ax^{2}+bx+c$(a,b,c为常数且$a+b+c= 10$)与多项式$(A-B)$互为“孪生多项式”,它们的“孪生式”的取值与x无关,直接写出满足条件的多项式C.

答案：
(1)①组多项式不是互为"孪生多项式".理由如下:因为(5x²-3)+(5x²+2)=5x²-3+5x²+2=10x²-1,10x²-1不是单项式,所以①组多项式不是互为"孪生多项式".
②组多项式是互为"孪生多项式".因为(ab²+a²b+1)+(-2a²b-ab²-1)=ab²+a²b+1-2a²b-ab²-1=-a²b,-a²b是单项式,所以②组多项式是互为"孪生多项式",它们的"孪生式"为-a²b.
(2)因为A=2x²-2x+3m与B=nx²+4x+1互为"孪生多项式",所以A+B=2x²-2x+3m+nx²+4x+1=(n+2)x²+2x+(3m+1)为单项式,所以n+2=0,3m+1=0,所以m=-1/3,n=-2,所以m+n=-7/3.
(3)C=-4x²+6x+8. 提示:因为m=-1/3,n=-2,所以A=2x²-2x+3m=2x²-2x-1,B=nx²+4x+1=-2x²+4x+1,所以A-B=(2x²-2x-1)-(-2x²+4x+1)=4x²-6x-2,因为C=ax²+bx+c与多项式(A-B)互为"孪生多项式",它们的"孪生式"的取值与x无关,所以(A-B)+C=4x²-6x-2+ax²+bx+c=(a+4)x²+(b-6)x+(c-2)为单项式,且该单项式为常数,所以a+4=0,b-6=0,所以a=-4,b=6,因为a+b+c=10,所以c=8,所以C=-4x²+6x+8.