《2025年小题狂做七年级数学上册苏科版巅峰版》

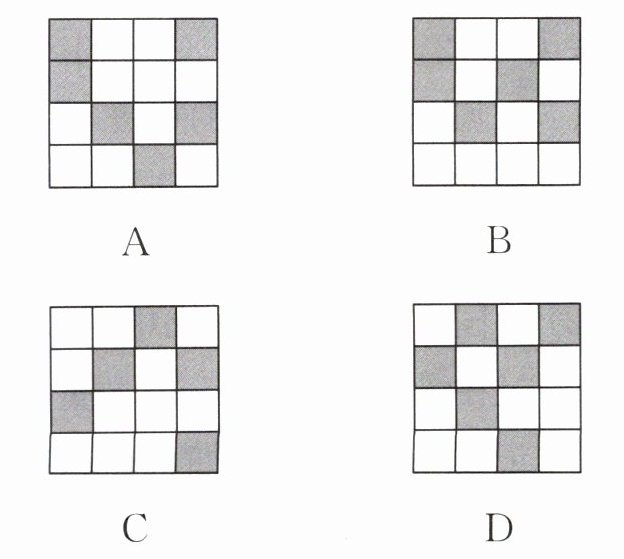
12. 二维码是用某种特定的、黑白相间的几何图形按一定规律分布在平面上的、记录数据符号信息的条码(如图1).某校利用二维码建立了一个身份识别系统,图2是某个学生的身份识别图案,其中第一行和第二行可分别转换为该学生的班级序号和学号.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,则$a×2^{3}+b×2^{2}+c×2^{1}+d$为该行所表示的数.例如:图2中第一行数字从左到右依次为0,1,0,1,计算得$0×2^{3}+1×2^{2}+0×2^{1}+1= 5$,表示该生为(5)班学生.请判断下列选项中表示(9)班学号为10的学生的身份识别图案是 (B)

答案： B 提示:选项A中,第二行所表示的数为$1×2^3+0×2^2+0×2^1+0 = 8$,学号不符合;选项B中,第一行所表示的数为$1×2^3+0×2^2+0×2^1+1 = 9$,第二行所表示的数为$1×2^3+0×2^2+1×2^1+0 = 10$,班级、学号均符合,故该选项符合题意;选项C中,第一行所表示的数为$0×2^3+0×2^2+1×2^1+0 = 2$,第二行所表示的数为$0×2^3+1×2^2+0×2^1+1 = 5$,班级、学号均不符合;选项D中,第一行所表示的数为$0×2^3+1×2^2+0×2^1+1 = 5$,班级不符合.

13. 【阅读学习】
计算:$1+5+5^{2}+5^{3}+…+5^{99}+5^{100}$.
观察发现,上式从第二项起,每一项都是它前一项的5倍.如果将上式各项都乘5,所得新算式中除个别项外,其余与原式中的项都相同,于是两式相减将使差易于计算.
解:设$S= 1+5+5^{2}+…+5^{99}+5^{100}$①,
则$5S= 5+5^{2}+5^{3}+…+5^{100}+5^{101}$②,
②-①,得$4S= 5^{101}-1$,则$S= \frac{5^{101}-1}{4}$,
即原式$=\frac{5^{101}-1}{4}$.
上面计算用的方法称为“错位相减法”.如果一列数,从第二项起每一项与前一项之比都相等(本例中都等于5),那么这列数的求和问题均可用上述“错位相减法”来解决.
【理解掌握】
(1)请你观察算式$1+\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+…+\frac{1}{2^{2025}}$是否具备上述规律？若具备,请你尝试用“错位相减法”计算上式的结果.
【灵活应用】
(2)已知$|x_{1}-1|+(x_{2}-2)^{2}+|x_{3}-3|+(x_{4}-4)^{4}+…+|x_{2025}-2025|+(x_{2026}-2026)^{2026}= 0$,则$2^{x_{1}}-2^{x_{2}}-2^{x_{3}}-…-2^{x_{2025}}+2^{x_{2026}}= $______.
解:
(1)具备上述规律.
设$S = 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots +\frac{1}{2^{2025}}$①,
则$\frac{1}{2}S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\cdots +\frac{1}{2^{2026}}$②,
① - ②,得$\frac{1}{2}S = 1-\frac{1}{2^{2026}}$,则$S = 2-\frac{1}{2^{2025}}$,即原式$=2-\frac{1}{2^{2025}}$.
(2)6

答案： 解:
(1)具备上述规律.
设$S = 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots +\frac{1}{2^{2025}}$①,
则$\frac{1}{2}S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\cdots +\frac{1}{2^{2026}}$②,
① - ②,得$\frac{1}{2}S = 1-\frac{1}{2^{2026}}$,则$S = 2-\frac{1}{2^{2025}}$,即原式$=2-\frac{1}{2^{2025}}$.
(2)6 提示:因为$|x_1 - 1|+(x_2 - 2)^2+|x_3 - 3|+(x_4 - 4)^4+\cdots +|x_{2025}-2025|+(x_{2026}-2026)^{2026}=0$,且$|x_1 - 1|\geq 0$,$(x_2 - 2)^2\geq 0$,$|x_3 - 3|\geq 0$,$(x_4 - 4)^4\geq 0$,$\cdots$,$|x_{2025}-2025|\geq 0$,$(x_{2026}-2026)^{2026}\geq 0$,所以$x_1 - 1 = 0$,$x_2 - 2 = 0$,$x_3 - 3 = 0$,$x_4 - 4 = 0$,$\cdots$,$x_{2025}-2025 = 0$,$x_{2026}-2026 = 0$,解得$x_1 = 1$,$x_2 = 2$,$x_3 = 3$,$\cdots$,$x_{2026}=2026$,所以原式$=2^1-2^2-2^3-2^4-\cdots-2^{2025}+2^{2026}=2^1+2^1-(2^1+2^2+\cdots+2^{2025})+2^{2026}$.设$S = 2^1+2^2+\cdots +2^{2025}$①,所以$2S = 2^2+2^3+\cdots +2^{2026}$②,② - ①,得$S = 2^{2026}-2^1$,所以原式$=4-(2^{2026}-2)+2^{2026}=6$.