《2025年小题狂做七年级数学上册苏科版巅峰版》

9. 某车站在检票前若干分钟就开始排队,排队的人数按一定的速度增加.若开放一个检票口,则要20 min检票口前的队伍才消失;若同时开放两个检票口,则8 min队伍就消失.设检票的速度是一定的.若同时开放三个检票口,则队伍消失要几分钟?

答案： 解:设检票开始时,等候检票的队伍有a人,每个检票口每分钟检票x人,队伍每分钟增加y人,则a/(x-y)=20,a/(2x-y)=8,所以20(x-y)=8(2x-y),解得x=3y.所以同时开放三个检票口,等候检票的队伍消失的时间是a/(3x-y)=20(x-y)/(3x-y)=20(3y-y)/(3×3y-y)=20×2/8=5(min).所以若同时开放三个检票口,则队伍消失要5 min.

10. 某校举行了主题为“扛红旗、当先锋、学党史”的知识竞赛,一共有30道题,每答对一题得4分,答错或不答扣2分.
(1) 小明参加了此竞赛,得90分,则他答对了多少道题?
(2) 小刚也参加了此竞赛,考完后自信满满,说:“这次竞赛我会得100分!”你认为可能吗?并说明理由.

答案：
(1)设小明答对了x道题.根据题意,得4x-2(30-x)=90,解得x=25.所以小明答对了25道题.
(2)不可能.理由如下:
设小刚答对了y道题.若他的得分是100分,则4y-2(30-y)=100,解得y=80/3.因为y不能为分数,所以小刚不可能得100分.

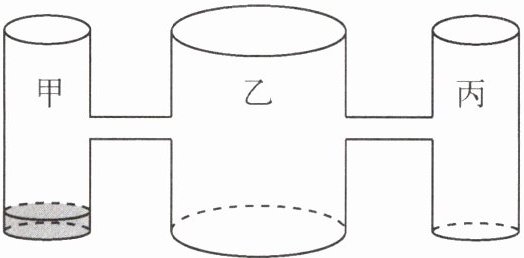
11. 如图,水平桌面上有甲、乙、丙三个圆柱形容器(足够高),底面半径之比为1:2:1,用两根相同的管子在容器的5 cm高度处连接(即管子底端离容器底5 cm),现三个容器中,只有甲中有水,水位高1 cm.若每分钟同时向乙和丙较为缓慢地注入相同量的水,注水1 min时,乙的水位高度为$\frac{5}{6}$cm,则当甲与乙的水位高度之差是0.5 cm时,注水时间为______min.


$\frac{3}{5}$或$\frac{33}{20}$或$\frac{171}{40}$

答案： 3/5或33/20或171/40 提示:由题意可知,注水1 min,乙的水位上升5/6 cm,丙的水位上升10/3 cm.设开始注入t min的水量后,甲与乙的水位高度之差是0.5 cm,有三种情况:①当乙的水位低于甲的水位时,有1-5/6 t=0.5,解得t=3/5.②当甲的水位低于乙的水位,且甲的水位不变时,由5/6 t-1=0.5,解得t=9/5.因为10/3×9/5=6(cm)＞5 cm,所以此时丙容器已向乙容器注水.因为5÷10/3=3/2(min),5/6×3/2=5/4(cm),所以5/4+2×5/6(t-3/2)-1=0.5,解得t=33/20.③当甲的水位低于乙的水位且乙的水位到达管子底端而甲的水位上升时,因为乙的水位到达管子底端的时间为3/2+(5-5/4)÷5/6÷2=15/4(min),所以5-1-2×10/3(t-15/4)=0.5,解得t=171/40.

12. 有一些相同的房间需要粉刷.一天3名师傅去粉刷8个房间,结果有$40m^2$墙面还没来得及粉刷;同样的时间内5名徒弟粉刷了9个房间的墙面.已知每名师傅比徒弟一天多粉刷$30m^2$的墙面.
(1) 求每个房间需要粉刷的墙面面积.
(2) 张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,则需要几天完成?
(3) 已知每名师傅、徒弟每天的工资分别是350元、280元,张老板要求在3天内完成36个这样的房间的粉刷任务,则在这8个人中雇用人员的最少费用是多少?(被雇用工人必须同时开工,同时收工)

答案：
(1)设每名徒弟一天粉刷的面积为x m²,则每名师傅一天粉刷的面积为(x+30)m².根据题意,得(3(x+30)+40)/8=5x/9,解得x=90.所以5x/9=50(m²),所以每个房间需要粉刷的墙面面积为50 m².
(2)由
(1)可知,每名徒弟一天粉刷的面积为90 m²,每名师傅一天粉刷的面积为120 m².所以请1名师傅带2名徒弟去,需要36×50/(120+90×2)=6(天)完成.
(3)若想在3天内完成,则每天粉刷的面积最少为36×50/3=600(m²).雇佣3个师傅和3个徒弟时,每天粉刷的面积是3×(120+90)=630(m²)＞600(m²),费用是3×3×(350+280)=5670(元);雇佣2个师傅和4个徒弟时,每天粉刷的面积是2×120+4×90=600(m²),费用是3×(2×350+4×280)=5460(元);雇佣1个师傅和5个徒弟时,每天粉刷的面积是1×120+5×90=570(m²)＜600(m²),不符合要求.所以在这8个人中,雇佣2个师傅和4个徒弟费用最少,最少费用为5460元.