《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 如图,∠1和∠2互补,则∠2与$\frac{1}{2}(∠1-∠2)$之间的关系是 (B)

A.互补
B.互余
C.和为$45^{\circ }$
D.和为$22.5^{\circ }$

答案： B

2. 下列说法中,正确的有 (B)
①由两条射线组成的图形叫作角；
②角的大小与边的长短无关,只与两条边张开的角度有关；
③角的两边是两条射线；
④把一个角放到一个放大10倍的放大镜下观看,角的度数也扩大10倍.
A.1个
B.2个
C.3个
D.4个

答案： B

3. 如图1中有1个角,图2中有3个角,图3中有6个角……以此类推,图n中角的个数是 (C)
A.$\frac{(n-1)(n-2)}{2}$
B.$\frac{n(n-1)}{2}$
C.$\frac{n(n+1)}{2}$
D.$\frac{(n+1)(n+2)}{2}$

答案： C

4. 已知两个角α,β都是钝角,若四个人根据α,β的数值计算出$\frac{1}{6}(α+β)的结果分别为26^{\circ },53^{\circ },60^{\circ },91^{\circ }$,尽管不知道α,β的数值,但可确定其中错误的结果有 (C)
A.1个
B.2个
C.3个
D.4个

答案： C 提示:因为α,β都是钝角,所以90°＜α＜180°,90°＜β＜180°,所以180°＜α+β＜360°,则30°＜$\frac{1}{6}$(α+β)＜60°,所以只有53°正确.

5. 某教科局提出开展“三有课堂”,在某中学一节体现“三有课堂”公开展示课上,李老师展示了一幅图,条件是:C为直线AB上一点,$∠DCE$为直角,CF平分$∠ACD$,CH平分$∠BCD$,CG平分$∠BCE$,各个小组经过讨论后得到以下结论:①$∠ACF与∠BCH$互余;②$∠FCG与∠HCG$互补;③$∠ECF与∠HCG$互补;④$∠ACD-∠BCE= 90^{\circ }$.其中正确的结论有 (C)
A.1个
B.2个
C.3个
D.4个

答案： C 提示:因为CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,所以∠ACF=∠FCD=$\frac{1}{2}$∠ACD,∠DCH=∠HCB=$\frac{1}{2}$∠DCB,∠BCG=∠ECG=$\frac{1}{2}$∠BCE.因为∠ACB=180°,∠DCE=90°,所以∠FCH=90°,∠HCG=45°,所以∠FCG=135°.所以∠ACF+∠BCH=90°,∠FCG+∠HCG=180°,故①②正确.又因为∠FCG＜∠ECF,所以∠ECF与∠HCG不互补,故③错误.易知∠ACD-∠BCE=180°-∠DCB-∠BCE=90°,故④正确.综上所述,正确的结论有①②④,共3个.

6. 当钟面上显示2时32分时,时针与分针的夹角是116°.

答案： 116° 提示:分针每分钟转6°,旋转32分钟,共计6°×32=192°,时针每小时转30°,每分钟转0.5°.共计30°×2+0.5°×32=76°,所以时针与分针的夹角为192°-76°=116°.

7. 用一副三角板可以画出的锐角总共有5个.

答案： 5 提示:用一副三角板可以画出的锐角有15°,30°,45°,60°,75°,共5个.

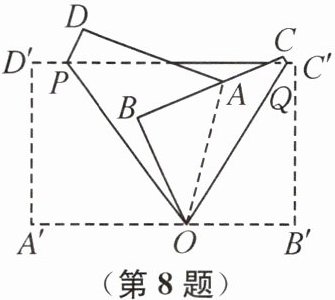
8. 如图,取一张长方形纸片,按图中所示的方法先折叠一角,得到折痕PO,再折叠另一角,得到折痕QO.若两折痕的夹角$∠POQ= 70^{\circ }$,则$∠AOB= $______40°.

答案： 40° 提示:设∠AOB=x°,∠POB=m°,∠AOQ=n°.由折叠可知∠POA'=∠POA=(m+x)°,∠B'OQ=∠BOQ=(n+x)°.因为∠POQ=70°,所以m+n+x=70.因为∠B'OA'=180°,所以(m+x)+(m+x+n)+(n+x)=180,即2(m+n+x)+x=180,所以x=40,所以∠AOB=40°.

9.(南京市联合体期末)如图,OC,OD是$∠AOB$内部的两条射线,OE平分$∠AOC$,OF平分$∠DOB$.若$∠EOF= m^{\circ },∠BOC= n^{\circ }$,则$∠AOD= $2m-n°(用含m,n的代数式表示).

答案： (2m-n) 提示:因为OE平分∠AOC,OF平分∠DOB,所以∠AOC=2∠COE,∠DOB=2∠DOF,所以∠AOB=∠AOC+∠COD+∠DOB=2∠COE+2∠DOF+∠COD=2∠EOF-∠COD.因为∠EOF=m°,∠BOC=n°,所以∠AOB=2m°-∠COD,所以∠AOD=∠AOB-∠DOB=2m°-∠COD-∠DOB=2m°-∠BOC=(2m-n)°.