《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 已知$a + b= \frac{1}{2}$,$a + c= -2$,那么代数式$(b - c)^{2}-2(c - b)-\frac{9}{4}$的值为(D)
A.-1
B.0
C.3
D.9

答案： D 提示:因为a+b= $\frac{1}{2}$,a+c=-2,所以(a+b)-(a+c)= $\frac{1}{2}$-(-2)= $\frac{5}{2}$,即b-c= $\frac{5}{2}$,c-b=- $\frac{5}{2}$,所以原式=( $\frac{5}{2}$)²-2×(- $\frac{5}{2}$)- $\frac{9}{4}$=9.

2. 如图,已知长方形的长为$a$、宽为$b$(其中$a ＞ b$),将这个长方形分别绕它的长和宽所在的直线旋转一周,得到两个圆柱甲、乙,则这两个圆柱的侧面积和体积的关系为(D)
A.甲、乙的侧面积不相同,体积也不相同
B.甲、乙的侧面积相同,体积也相同
C.甲、乙的侧面积不相同,体积相同
D.甲、乙的侧面积相同,体积不同

答案： D 提示:甲圆柱的侧面积为2abπ,体积为ab²π;乙圆柱的侧面积为2abπ,体积为ba²π.因为a＞b,所以a²bπ≠ab²π,故甲、乙的侧面积相同,体积不同.

3. 用一元一次方程的知识,可把无限循环小数化为分数,例如:把$0.\dot{1}$化为分数,设$x = 0.\dot{1}$.两边同时乘以10,得$10x= 1.\dot{1}$,$10x = 1+0.\dot{1}$,即$10x= 1 + x$.移项、合并同类项,得$9x = 1$,解得$x= \frac{1}{9}$,即$0.\dot{1}= \frac{1}{9}$.把$1.\dot{2}\dot{5}$化为分数是(D)
A.$1\frac{1}{4}$
B.$\frac{125}{99}$
C.$1\frac{1}{5}$
D.$1\frac{25}{99}$

答案： D 提示:设1. $\dot{2}\dot{5}$=y.两边同时乘以100,得100y=125. $\dot{2}\dot{5}$,所以100y=124+1. $\dot{2}\dot{5}$,即100y=124+y.移项、合并同类项,得99y=124,解得y=1 $\frac{25}{99}$.

4. 如图,在两个形状、大小完全相同的大长方形中分别放入四个相同的小长方形.如果大长方形的宽为$a$,那么图2与图1的阴影部分周长之差是(C)
A. $\frac{1}{2}a$
B. $\frac{3}{4}a$
C. $\frac{4}{3}a$
D. $a$

答案： C 提示:由题图2可知,小长方形的宽为 $\frac{a}{3}$.再结合题图1可知,小长方形的长为 $\frac{2}{3}$a,所以大长方形的长为 $\frac{2}{3}$a+ $\frac{a}{3}$×2= $\frac{4}{3}$a,所以题图1中阴影部分的周长C₁=2[ $\frac{4}{3}$a+(a-2× $\frac{a}{3}$)]= $\frac{10}{3}$a,题图2中阴影部分的周长C₂=2( $\frac{4}{3}$a- $\frac{2}{3}$a+a+ $\frac{2a}{3}$)= $\frac{14}{3}$a,所以C₂-C₁= $\frac{4}{3}$a.

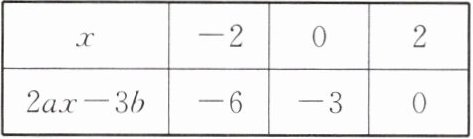
5. 整式$2ax-3b$($a$,$b$为常数,$a\neq0$)的值随$x$的取值不同而不同,下表是当$x$取不同值时对应的整式的值,则关于$x的方程-\frac{ax}{3}+\frac{b}{2}= \frac{1}{2}$的解是 $x=0$.
| $x$ | $-2$ | $0$ | $2$ |
| $2ax-3b$ | $-6$ | $-3$ | $0$ |

答案： x=0 提示:原方程可化为2ax-3b=-3.由题表可知,当x=0时,2ax-3b=-3,即x=0是原方程的解.

6. 已知关于$x的一元一次方程\frac{x}{2024}+5 = 2024x+m的解为x = 2025$,那么关于$y的一元一次方程\frac{5 - y}{2024}-5= 2024(5 - y)-m$的解为2030.

答案： y=2030 提示:方程 $\frac{5-y}{2024}$-5=2024(5-y)-m可化为 $\frac{-(y-5)}{2024}$-5=-2024(y-5)-m,即 $\frac{y-5}{2024}$+5=2024(y-5)+m.因为关于x的一元一次方程 $\frac{x}{2024}$+5=2024x+m的解为x=2025,所以设y-5=x,则方程 $\frac{y-5}{2024}$+5=2024(y-5)+m的解为y-5=2025,解得y=2030.

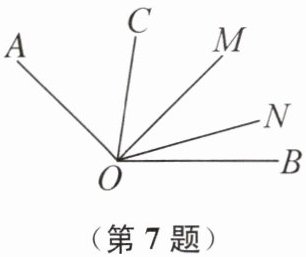
7. 如图,若$\angle AOB= m^{\circ}$,$\angle AOM= n^{\circ}$,$\angle BOC = 4\angle BON$,$OM平分\angle CON$,则$\angle MON= $$\frac{3}{5}(m - n)$°(用含$m$,$n$的代数式表示).

答案： $\frac{3}{5}$(m - n)° 提示:由题意,得∠CON=3∠BON.因为OM平分∠CON,所以∠MON= $\frac{1}{2}$∠CON= $\frac{3}{2}$∠BON,所以∠BON= $\frac{2}{3}$∠MON.所以∠BOM=∠MON+∠BON= $\frac{5}{3}$∠MON.易得∠BOM=∠AOB-∠AOM=(m - n)°.所以∠MON= $\frac{3}{5}$(m - n)°.

8. 周末,小丽和小红相约爬山(山脚处的点$A$,$B$在同一水平线上).她们从南坡山脚点$A$处出发上行,在南坡的点$E$处休息片刻后,继续登山到达坡顶点$C$处观光游玩,之后沿北坡下山,至北坡山脚点$B$处.已知南北两坡长度不相等,可以分别看作线段$AC$,$BC$,$E为AC$的中点,且$EC = 200m$,点$D$平分南北两坡总长,且$CD = 20m$,则北坡$BC$的长度是360或440m.

答案： 360或440 提示:由题意,得AE=EC=200m,AC=AE+EC=400m.当点D在AC上时,因为CD=20m,所以AD=AC-CD=380m.此时CD+BC=AD=380m,所以BC=360m.当点D在BC上时,BD=AC+CD=420m,所以BC=BD+CD=440m.

9. 对正整数$n$反复进行下列两种运算:①若$n$是偶数,就除以2;②若$n$是奇数,就乘3加1.例如:正整数6经过一次操作后的结果是3,经过两次操作后的结果是10.若某正整数$m$经过四次操作后的结果是2,则正整数$m$的值是32或5或4.

答案： 32或5或4 提示:第4步运算前的数为2×2=4或(2-1)÷3= $\frac{1}{3}$(不合题意,舍去),所以第3步运算前的数为4×2=8或(4-1)÷3=1.当第3步运算前的数为8时,第2步运算前的数为8×2=16或(8-1)÷3= $\frac{7}{3}$(不合题意,舍去),此时第1步运算前的数为16×2=32或(16-1)÷3=5.当第3步运算前的数为1时,第2步运算前的数为1×2=2或(1-1)÷3=0(不合题意,舍去),此时第1步运算前的数为2×2=4或(2-1)÷3= $\frac{1}{3}$(不合题意,舍去).故正整数m的值是32或5或4.