《2025年小题狂做七年级数学上册苏科版巅峰版》

12. 一只电子青蛙要从点A跳到点B,以平均2 dm/s的速度跳跃. 它先前进1 dm,再后退2 dm；又前进3 dm,再后退4 dm……每次跳跃都在A,B两点所在的直线上.
(1)5 s时它距离点A多远？
(2)若A,B两点相距30 dm,则它可能到达点B吗？若能,则它第一次到达点B需要多长时间？若不能,请说明理由.

答案： 解:
(1)5 s时青蛙跳跃的总路程为$2×5=10(\text{dm})$,这10 dm正好是青蛙先前进1 dm,再后退2 dm,又前进3 dm,再后退4 dm的总路程.记青蛙从点A开始前进为正,后退为负,则有$1+(-2)+3+(-4)=1-2+3-4=-2(\text{dm})$,所以此时青蛙距离点A 2 dm.
(2)由
(1)可得青蛙每跳奇数次会从点A向点B前进1 dm.因为A,B两点相距30 dm,所以青蛙要跳$30×2-1=59$(次)才可以到达点B,所以总路程为$1+2+3+\cdots+59=(1+59)×59÷2=1 770(\text{dm})$,所用时间为$1 770÷2=885(\text{s})$.所以它第一次到达点B需要885 s.

13. 定义$a*b= 3a-b$,$a⊕b= b-a^{2}$. 现有下列结论：①$3*2= 11$；②$2⊕(-1)= -5$；③$(\frac{1}{3}*\frac{2}{5})⊕(\frac{7}{2}⊕\frac{1}{4})= -\frac{291}{25}$；④若$a*b= b*a$,则a= b. 其中结论正确的有(B)
A.1个
B.2个
C.3个
D.4个

答案： B

14. 平平和安安进行摸球游戏,如图,框1中有A,B两个大小相同的球,框2中有C,D,E,F四个大小相同的球,游戏规则为先从框1中摸出一个球,再从框2中将4个球全部摸出,并根据从框2中摸出的球,将从框1中摸出的球上的数字按顺序进行计算.

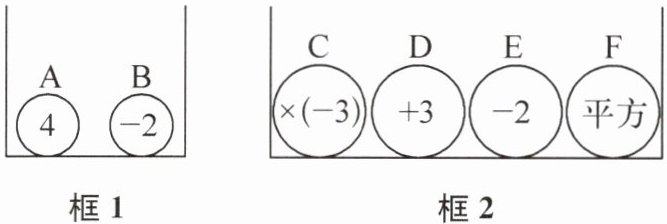
(1)平平从框1中摸出了球A,从框2中摸出球的顺序为D→E→C→F,请你帮助平平求出计算结果.225
(2)①若安安从框1中摸出了球B,从框2中摸出球的顺序为F→E→______→______,计算结果为-3,请你通过计算判断安安从框2中摸出球的顺序.CD
②若安安从框1中摸出了球A,从框2中先摸出的球为球D,则摸球游戏计算的最大结果是多少？请你写出计算过程.由题意可得,当摸出球的顺序为D→C→E→F时,摸球游戏计算的结果最大,最大结果是[(4+3)×(-3)-2]²=[7×(-3)-2]²=(-21-2)²=(-23)²=529

答案： 解:
(1)由题意可得,计算结果为$[(4+3-2)×(-3)]^{2}=[5×(-3)]^{2}=(-15)^{2}=225$.
(2)①C D 提示:若摸出球的顺序为F→E→D→C时,计算结果为$[(-2)^{2}-2+3]×(-3)=(4-2+3)×(-3)=5×(-3)=-15$;若摸出球的顺序为F→E→C→D时,计算结果为$[(-2)^{2}-2]×(-3)+3=(4-2)×(-3)+3=2×(-3)+3=-6+3=-3$.所以计算结果为-3时,摸球顺序为F→E→C→D.
②由题意可得,当摸出球的顺序为D→C→E→F时,摸球游戏计算的结果最大,最大结果是$[(4+3)×(-3)-2]^{2}=[7×(-3)-2]^{2}=(-21-2)^{2}=(-23)^{2}=529$.