《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 下列语句正确的是 (B)
A.如果两条直线都和第三条直线垂直,那么这两条直线平行
B.同一平面内,若三条直线只有两个交点,则这三条直线中必有两条直线互相平行
C.两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线平行
D.过一点有且只有一条直线与已知直线平行

答案： B

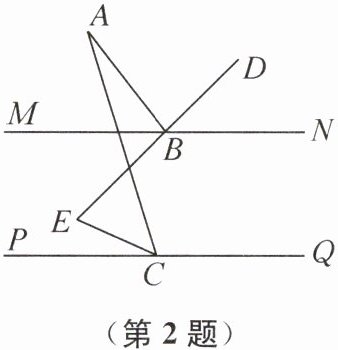
2. 如图,MN//PQ,点 B 在 MN 上,点 C 在 PQ 上,点 A 在 MN 上方,点 E 在 BD 的反向延长线上,且∠ABD：∠DBN= 3：2,∠ACE：∠ECP= 3：2,设∠A= α,则∠E 的度数用含α的式子一定可以表示为 ( )

A.2α
B.72°+$\frac{2}{5}$α
C.108°-$\frac{3}{5}$α
D.90°-α

答案：
B 提示:如图，过点A作AG//MN,过点E作EH//MN,因为MN//PQ,所以MN//PQ//AG//EH。因为∠ABD:∠DBN = 3:2,∠ACE:∠ECP = 3:2,所以设∠ABD = 3x,∠ACE = 3y,则∠DBN = 2x,∠ECP = 2y。因为MN//PQ//AG//EH,所以∠BEH = ∠DBN = 2x,∠HEC = ∠ECP = 2y,∠GAB = 180°−(∠DBN + ∠ABD)=180°−5x,∠GAC = ∠ACP = ∠ACE + ∠ECP = 5y。所以∠DEC = ∠BEH + ∠HEC = 2(x + y),∠CAB = ∠GAC−∠GAB = 5(x + y)−180° = α,所以x + y = $\frac{180° + α}{5}$ = 36° + $\frac{1}{5}$α,所以∠DEC = 2(x + y)=72° + $\frac{2}{5}$α。

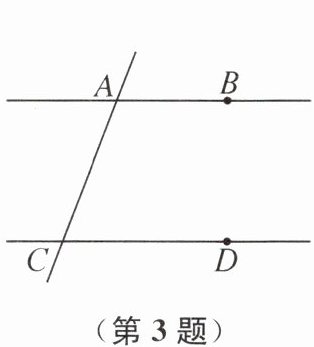
3. (扬州市仪征市期末)如图,已知直线 AB,CD 被直线 AC 所截,AB//CD,E 是平面内任意一点(点 E 不在直线 AB,CD,AC 上),设∠BAE= α,∠DCE= β.现给出下列各式：①α+β,②α-β,③β-α,④180°-α-β.则∠AEC 的度数可能是 ( )

A.①②③
B.①②④
C.②③④
D.①②③④

答案：
A 提示:如图1,由AB//CD,得∠AOC = ∠DCE₁ = β,所以∠AE₁C = 180°−∠AOE₁−∠BAE₁ = ∠AOC−∠BAE₁ = β−α;如图2,过点E₂作AB的平行线,则∠1 = ∠BAE₂ = α,∠2 = ∠DCE₂ = β,所以∠AE₂C = α + β;如图3,由AB//CD,得∠BOE₃ = ∠DCE₃ = β,所以∠AE₃C = 180°−∠DAE₃−∠BOE₃ = ∠BAE₃−∠BOE₃ = α−β;如图4,由AB//CD,得∠BAC + ∠DCA = 180°,所以∠BAE₄ + ∠AE₄C + ∠DCE₄ = 360°,所以∠AE₄C = 360°−α−β;当点E在CD的下方时，同理可得∠AEC = α−β或∠AEC = β−α。

4. 如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的∠A 是 120°,第二次拐的∠B 是 150°,第三次拐的是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C 的大小是 (A)
A.150°
B.130°
C.140°
D.120°

答案： A 提示:过点B作BE//AM(点E在点B上方)。因为AM//CN,所以AM//BE//CN,所以∠A = ∠ABE。因为∠A = 120°,所以∠ABE = 120°。因为∠ABC = 150°,所以∠EBC = ∠ABC−∠ABE = 150°−120° = 30°,所以∠C = 180°−30° = 150°。

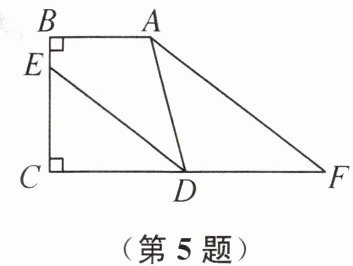
5. 如图,AB⊥BC 于点 B,DC⊥BC 于点 C,DE 平分∠ADC,交 BC 于点 E,F 为线段 CD 延长线上一点,∠BAF= ∠EDF,现有下列结论：①∠BAD+∠ADC= 180°；②AF//DE；③∠DAF= ∠F；④若 CD= DF,则 DE= AF.其中正确的是①②③(填序号).

答案： ①②③ 提示:因为AB⊥BC于点B,DC⊥BC于点C，所以AB//CD，所以∠BAD + ∠ADC = 180°,故①正确;因为AB//CD,所以∠AFD + ∠BAF = 180°,因为∠BAF = ∠EDF,所以∠AFD + ∠EDF = 180°,所以AF//DE,故②正确;可知∠DAF = ∠ADE,∠F = ∠CDE,因为DE平分∠ADC交BC于点E,所以∠ADE = ∠CDE,所以∠DAF = ∠F,故③正确;由CD = DF无法得出DE = AF,故④不正确。

6. 如图,已知 AB//CD,∠EAF= $\frac{1}{3}$∠BAF,∠ECF= $\frac{1}{3}$∠DCF,记∠AEC= m∠AFC,则 m= $\frac{4}{3}$.

答案： $\frac{4}{3}$ 提示:分别过点E,F作直线EM//AB,FN//AB(点M,N均在点E左侧)。因为AB//CD,所以AB//EM//FN//CD。因为∠EAF = $\frac{1}{3}$∠BAF,∠ECF = $\frac{1}{3}$∠DCF,所以∠AEC = 4∠EAF + 4∠ECF,∠AFC = 3∠EAF + 3∠ECF。因为∠AEC = m∠AFC,所以m = $\frac{∠AEC}{∠AFC}$ = $\frac{4}{3}$。

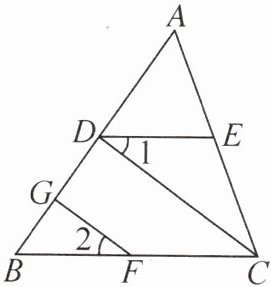
7. 如图,已知 FG⊥AB,CD⊥AB,垂足分别为 G,D,∠1= ∠2,试判断∠CED 与∠ACB 之间的数量关系,并说明理由.

答案： 解:∠CED + ∠ACB = 180°。理由如下:因为FG⊥AB,CD⊥AB，垂足分别为G,D,所以∠FGB = ∠CDB = 90°,所以GF//CD,所以∠2 = ∠BCD。又因为∠1 = ∠2,所以∠1 = ∠BCD,所以DE//BC,所以∠CED + ∠ACB = 180°。