《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空。”诗中后面两句的意思是：如果一间客房住7人,那么有7人无房可住；如果一间客房住9人,那么就空出一间客房。若设该店有客房x间,则列出关于x的一元一次方程正确的是(B)
A.7x-7= 9(x-1)
B.7x+7= 9(x-1)
C.7x-7= 9x-1
D.7x+7= 9x-1

答案： B

2. 如图,按照程序图计算,当输入正整数x时,输出的结果为215,则输入的x值不可能是(A)
A.5
B.7
C.23
D.71

答案： A 提示:如果输入的数经过一次运算就能输出结果,则3x+2=215,解得x=71;如果输入的数字经过两次运算才能输出结果,则第1次计算后的结果是71,于是3x+2=71,解得x=23;如果输入的数字经过三次运算才能输出结果,则第2次计算后的结果是71,第1次计算后的结果是23,于是3x+2=23,解得x=7;如果输入的数字经过四次运算才能输出结果,则第1次计算后的结果是7,于是3x+2=7,解得x=5/3,此时x不是正整数,舍去.综上所述,输入的x的值可能是71,23,7.

3. 某人下午6点多外出时,看手表两指针的夹角为110°,下午7点前回家发现两指针的夹角仍为110°,则他外出的时间为(C)
A.30 min
B.35 min
C.40 min
D.45 min

答案： C 提示:由题可知,6点多外出时,分针没有追上时针,7点前回家时,分针追上并超过时针.由于时针和分针1 min旋转的角度分别是0.5°和6°,并分别设外出和回家时的时刻为6点x分和6点y分,则180+0.5x-6x=110,6y-180-0.5y=110,解得x=140/11,y=580/11,所以外出的时间为580/11-140/11=40(min).

4. 有一台功能特殊的计算器,对任意两个整数只能完成求差后再取绝对值的运算,其运算过程是：输入第一个整数$x_1,$只显示不运算,接着再输入整数$x_2$后则显示|$x_1-x_2$|的结果。比如依次输入1,2,则输出的结果是|1-2|= 1；此后每输入一个整数都是与前次显示的结果进行求差后再取绝对值的运算。有下列说法：
①依次输入1,2,3,4,则最后输出的结果是2；
②若将2,3,6,9这4个整数任意地一个一个输入,全部输入完毕后显示的结果的最大值是8；
③若将1,2,3,…,2025这2025个整数任意地一个一个输入,全部输入完毕后显示的结果的最大值是2025。以上说法正确的个数是(D)
A.0
B.1
C.2
D.3

答案： D 提示:①由题意,可得|1-2|=|-1|=1,|1-3|=|-2|=2,|2-4|=|-2|=2,最后输出的结果是2,故①正确;②易知输入的数为正整数时,显示的结果一定小于或等于该正整数,对于2,3,6,9,易得结果最大值一定小于或等于9,此时,正整数9必须最后输入,且前三个数显示结果为零.枚举可知,2,3,6无法得到结果0,当按3,6,2,9的顺序输入时,可得|3-6|=3,|3-2|=1,|1-9|=8,全部输入完毕后显示的结果的最大值是8,故②正确;③同②可得这2025个正整数输入后显示的结果最大值小于或等于2025,分析可得,四个连续正整数x,x+1,x+2,x+3按x,x+2,x+3,x+1的顺序输入后,结果为0,故可先每四个数一组,将前2024个数输入,使得输出结果为0,再输入2025,即依次输入1,3,4,2;5,7,8,6;9,11,12,10;……;2021,2023,2024,2022;2025;根据运算规律可得结果是2025,故③正确.

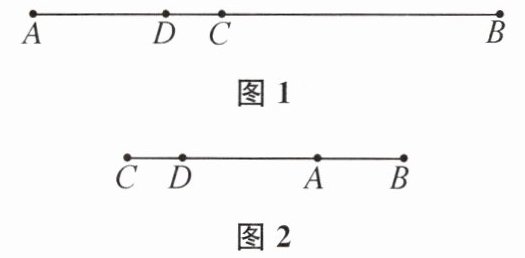
5. 如图1,AB是一条拉直的细绳,C和D两点在AB上,且AC：BC= 2：3,AD：BD= 3：7。若将点C固定,将AC折向BC,使得AC重叠在BC上(如图2),再沿点D剪断,使细绳分成三条,则分成的三条细绳的长度由小到大之比为( )D

A.1:2:3
B.1:1:3
C.1:1:2
D.2:3:5

答案： D 提示:设对折后点D关于点C的对称点为D',被剪断两处分别是点D和点D',剪开的三段细绳依次是AD,DD',D'B.因为AC∶BC=2∶3,AC+CB=AB,所以AC=2/5AB,BC=3/5AB.因为AD∶BD=3∶7,AD+DB=AB,所以AD=3/10AB,所以CD=AC-AD=2/5AB-3/10AB=1/10AB,所以DD'=2CD=2×1/10AB=1/5AB.又因为AD=3/10AB,所以D'B=AB-AD-DD'=AB-3/10AB-1/5AB=1/2AB,所以DD'＜AD＜D'B.所以DD'∶AD∶D'B=1/5AB∶3/10AB∶1/2AB=2∶3∶5.

6. 如图,小明拿到一个没装满水的有盖可密封的正方体盒子,盒子可以采用任何方式放置,他不断改变盒子的放置方式,盒子里的水便形成不同的几何体,则下列选项中：①长方体,②正方体,③圆柱体,④三棱锥,⑤三棱柱,可能是盒子里的水形成的几何体的有①④⑤(填序号)。

答案： ①④⑤ 提示:假设在桌面上放置这个正方体盒子,以桌面为水平底面.①当正方体盒子水平放置,使其一整个面接触桌面时,水在盒子里可以形成长方体;②因为水没有装满盒子,所以无论怎样放置,都无法形成正方体;③正方体盒子的形状决定了水无法形成圆柱体;④将正方体盒子倾斜放置,使其仅有一个顶点接触桌面时,水在盒子里可以形成三棱锥;⑤将正方体盒子倾斜放置,使其仅有一条棱接触桌面时,水在盒子里可以形成三棱柱的形状.综上所述,可能是盒子里的水形成的几何体的有①长方体,④三棱锥,⑤三棱柱.

7. 如图,已知AB//CD,EF//BN,MN//DE,则∠ABF+∠E+∠F+∠EPN+∠M+∠N+∠CDM= 360°。

答案： 360° 提示:如图,过点P作PQ//AB.因为AB//CD,所以PQ//CD.因为EF//BN,所以∠F=∠FBP,∠E=∠EPB,∠E+∠EPN=180°.因为PQ//AB,所以∠BPQ=∠ABP=∠ABF+∠FBP=∠ABF+∠F.因为MN//DE,所以∠M=∠MDE,∠N=∠NPD.因为PQ//CD,所以∠DPQ=∠CDP=∠MDE+∠CDM=∠M+∠CDM,所以∠ABF+∠E+∠F+∠EPN+∠M+∠N+∠CDM=180°+∠BPQ+∠NPD+∠DPQ=360°.

8. 甲、乙两动点分别从正八边形ABCDEFGH的顶点A,G同时出发,沿正八边形的边移动。甲点依顺时针环形运动,乙点依逆时针环形运动。若乙的速度是甲的速度的3倍,则它们第2025次相遇在正八边形的边AH上(用字母表示)。

答案： AH 提示:设正八边形的边长为a,甲的速度为v,则乙的速度为3v.根据题意,得第一次相遇甲、乙走的总路程为2a,则第一次相遇的时间为2a/(v+3v)=a/(2v),此时甲走了a/(2v)×v=1/2a,即相遇在正八边形的边AH上;第二次相遇甲、乙走的总路程为8a,则第二次相遇的时间为8a/(v+3v)=2a/v,此时甲走了2a/v×v=2a,即相遇在正八边形的边GF上;第三次相遇甲、乙走的总路程为8a,则第三次相遇的时间为8a/(v+3v)=2a/v,此时甲走了2a/v×v=2a,即相遇在正八边形的边ED上;第四次相遇甲、乙走的总路程为8a,则第四次相遇的时间为8a/(v+3v)=2a/v,此时甲走了2a/v×v=2a,即相遇在正八边形的边CB上;第五次相遇甲、乙走的总路程为8a,则第五次相遇的时间为8a/(v+3v)=2a/v,此时甲走了2a/v×v=2a,即相遇在正八边形的边AH上……以此类推,第五次和第一次相同,所以相遇位置每四次一循环.因为2025÷4=506……1,所以第2025次相遇与第一次相同,在正八边形的边AH上.