《2025年小题狂做七年级数学上册苏科版巅峰版》

9. 如图,点O在直线EF上,射线OA,OB与射线OC,OD分别在直线EF两侧,且∠AOB= 120°,∠COD= 70°.
(1)如图1,若OC平分∠BOD,OE平分∠AOD,过点O作射线OG⊥OB,求∠EOG的度数.
(2)如图2,若在∠BOC内部作一条射线OH,使得∠COH:∠BOH= 2:3,∠DOE= 5∠FOH,试判断∠AOE与∠DOE的数量关系.

答案：
解:
(1)因为OC平分∠BOD,所以∠BOD=2∠COD=2×70°=140°,又因为∠AOB=120°,所以∠AOD=360°−∠AOB−∠BOD=360°−120°−140°=100°.因为OE平分∠AOD,所以∠AOE=$\frac{1}{2}$∠AOD=50°.如图1,当OG在EF下方时，因为OG⊥OB,所以∠BOG=90°,所以∠AOG=∠AOB−∠BOG=120°−90°=30°,所以∠EOG=∠AOG+∠AOE=80°.


如图2,当OG在EF上方时,因为OG⊥OB,所以∠BOG=90°,因为∠AOE+∠AOB+∠BOG+∠EOG=360°,所以∠EOG=360°−50°−120°−90°=100°.综上所述，∠EOG的度数为80°或100°.
(2)如图3，当OH在OF的上方时，设∠FOH=α,则∠DOE=5α,所以∠COH=180°−∠DOE−∠COD−∠FOH=110°−6α,因为∠COH:∠BOH=2:3,所以∠BOC=$\frac{5}{2}$∠COH=275°−15α,所以∠AOD=360°−∠COD−∠BOC−∠AOB=360°−70°−(275°−15α)−120°=15α−105°,所以∠AOE=∠AOD−∠DOE=10α−105°,所以∠AOE=2∠DOE−105°.当OH在OF 的下方时，同理可得∠COH=180°−∠DOE−∠COD+∠FOH=110°−4α,因为∠COH:∠BOH=2:3,所以∠BOC=$\frac{5}{2}$∠COH=275°−10α,所以∠AOD=360°−∠COD−∠BOC−∠AOB=360°−70°−(275°−10α)−120°=10α−105°,所以∠AOE=∠AOD−∠DOE=5α−105°,所以∠AOE=∠DOE−105°.综上所述,∠AOE=2∠DOE−105°或∠AOE=∠DOE−105°.

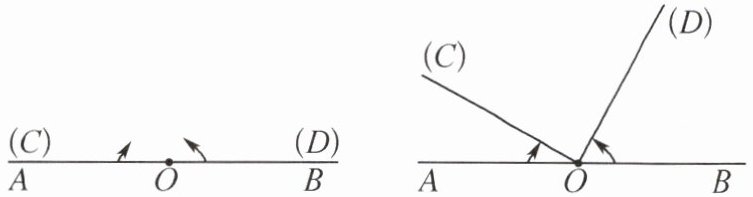
10. 如图,O是直线AB上一点,射线OC绕点O顺时针旋转,从OA出发,旋转速度为10°/s,射线OD绕点O逆时针旋转,从OB出发,旋转速度为20°/s,射线OC与OD同时旋转,设旋转的时间为t s,当OC旋转到与OB重合时,OC,OD都停止运动.
(1)当t= 2时,∠COD= 120°.
(2)当t= 3或9或15 时,OC⊥OD.

答案：
(1)120
(2)3或9或15　提示:在OC与OD重合之前,0≤t≤6,∠AOC=10t°,∠BOD=20t°,因为OC⊥OD,所以∠COD=90°,因为∠AOC+∠COD+∠BOD=180°,所以10t°+20t°+90°=180°,解得t=3;在OC与OD重合之后,OD到达OA之前(包含OA),6＜t≤9,∠AOC=10t°,∠BOD=20t°,因为OC⊥OD,所以∠COD=90°,此时∠AOC−∠COD+∠BOD=180°,所以10t°+20t°−90°=180°,解得t=9;在OA与OD重合之后,OC与OD的反向延长线重合前，∠AOC=10t°,∠AOD=20t°−180°,令10t°+20t°−180°=180°,解得t=12,所以9＜t≤12,因为∠COD=∠AOC+∠AOD=30t°−180°＞90°,所以OC不可能垂直于OD;当OC与OD的反向延长线重合后,OC到达OB之前,12＜t≤18,∠BOD=360°−20t°,∠BOC=180°−10t°,此时∠COD=∠BOC+∠BOD=180°−10t°+360°−20t°=540°−30t°,所以540°−30t°=90°,解得t=15.

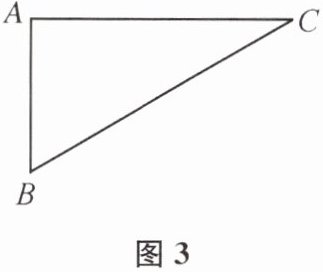
11. 如图1,将三角板ABC与三角板ADE摆放在一起,其中∠ACB= 30°,∠DAE= 45°,∠BAC= ∠D= 90°.如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE= α(0°＜α＜180°).
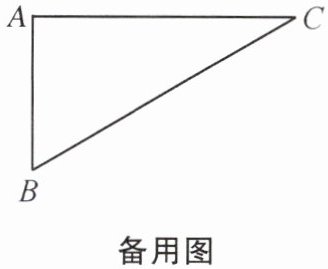
(1)当α= 105°时,AD⊥BC,并在图3中画出相应的图形.
(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系.
解：|∠CAD−∠BAE|=45°或∠CAD+∠BAE=45°.理由如下:当0°＜α＜45°时,∠CAD=45°−α,∠BAE=90°−α,所以∠BAE−∠CAD=45°.当45°≤α＜90°时,∠CAD=α−45°,∠BAE=90°−α,所以∠CAD+∠BAE=45°.当90°≤α＜180°时,∠CAD=α−45°,∠BAE=α−90°,所以∠CAD−∠BAE=45°.综上所述，在旋转过程中，∠CAD与∠BAE之间的关系为|∠CAD−∠BAE|=45°或∠CAD+∠BAE=45°.
(3)当三角板ADE旋转速度为5°/s,且它的一边与三角板ABC的某一边垂直时,直接写出时间t的所有取值.
3,9,12,18,21,27

答案： 解:
(1)105°　图略.
(2)|∠CAD−∠BAE|=45°或∠CAD+∠BAE=45°.理由如下:当0°＜α＜45°时,∠CAD=45°−α,∠BAE=90°−α,所以∠BAE−∠CAD=45°.当45°≤α＜90°时,∠CAD=α−45°,∠BAE=90°−α,所以∠CAD+∠BAE=45°.当90°≤α＜180°时,∠CAD=α−45°,∠BAE=α−90°,所以∠CAD−∠BAE=45°.综上所述，在旋转过程中，∠CAD与∠BAE之间的关系为|∠CAD−∠BAE|=45°或∠CAD+∠BAE=45°.
(3)满足题意的t的值有3,9,12,18,21,27　提示:在题中条件下,顺时针旋转会出现DE⊥BC,DE⊥AC,AE⊥BC,AE⊥AC,AD⊥BC,AD⊥AC,DE⊥AB七种垂直情况.当DE⊥BC时,α=15°,t=15÷5=3;当DE⊥AC 时,α=45°,t=45÷5=9;当AE⊥BC时,α=60°,t=60÷5=12;当AE⊥AC时,α=90°,t=90÷5=18;当AD⊥BC时,α=105°,t=105÷5=21;当AD⊥AC时,α=135°,t=135÷5=27;当DE⊥AB时,α=135°,t=135÷5=27.