《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 方程$|x-2025|= 2025-x$的解有(D)
A.1个
B.2个
C.3个
D.无数个

答案： D

2. 下列时刻中,时针和分针所成的角为$90^{\circ }$的是(D)
A.12时15分
B.11时10分
C.9时30分
D.3时

答案： D

3. 计算$(\frac {1}{2}-1)×(\frac {1}{3}-1)×(\frac {1}{4}-1)×... ×(\frac {1}{2024}-1)×(\frac {1}{2025}-1)$的结果为(D)
A.$\frac {2024}{2025}$
B.1
C.$-\frac {1}{2025}$
D.$\frac {1}{2025}$

答案： D 提示:原式$=(-\frac{1}{2})×(-\frac{2}{3})×(-\frac{3}{4})×\cdots×(-\frac{2023}{2024})×(-\frac{2024}{2025})=\frac{1}{2025}$.

4. 已知粗蜡烛和细蜡烛的长度一样,粗蜡烛可以点5h,细蜡烛可以点4h,如果同时点燃这两支蜡烛,过了一段时间后,剩余粗蜡烛的长度是细蜡烛长度的2倍,那么这两支蜡烛已点燃的时间是(C)
A.3h
B.3.2h
C.$\frac {10}{3}h$
D.3.5h

答案： C 提示:设这两支蜡烛已点燃的时间是$x\ \text{h}$.根据题意,得$1-\frac{x}{5}=2(1-\frac{x}{4})$,解得$x=\frac{10}{3}$.所以这两支蜡烛已点燃的时间是$\frac{10}{3}\ \text{h}$.

5. 如图,一张长方形纸片的长为m,宽为n($m＞3n$).先在其两端分别折出两个正方形(正方形ABEF,正方形CDGH)后展开,再分别将长方形ABHG,长方形CDFE对折,折痕分别为MN,PQ,则长方形MNQP的面积为(A)
A.$n^{2}$
B.$n(m-n)$
C.$n(m-2n)$
D.$\frac {nm}{3}$

答案： A 提示:由折叠的性质可知,$AF=DG=AB=CD=n$,所以$AG=DF=m-n$,则$AM=DP=\frac{m-n}{2}$,所以$MP=AD-AM-DP=m-2×\frac{m-n}{2}=n$,所以长方形$MNQP$的面积为$MP\cdot MN=n\cdot n=n^{2}$.

6. 新规定一种运算法则：$a※b= a^{2}+2ab$,若$(-2)※x= -2+x$,则x的值为$\frac{6}{5}$.

答案： $\frac{6}{5}$

7. 当$x= -2$时,代数式$ax^{5}+bx^{3}+cx-6$的值为8,则当$x= 2$时,代数式$ax^{5}+bx^{3}+cx-6$的值为-20.

答案： $-20$ 提示:把$x=-2$代入$ax^{5}+bx^{3}+cx-6=8$,得$-2^{5}a-2^{3}b-2c-6=8$,所以$2^{5}a+2^{3}b+2c=-8-6=-14$,所以当$x=2$时,$ax^{5}+bx^{3}+cx-6=2^{5}a+2^{3}b+2c-6=(-14)-6=-20$.

8. 小明在某月历上圈出如图所示的呈十字形的5个数,如果圈出的5个数的和为65,那么其中最小的数为6.

答案： 6 提示:根据题意,可设呈十字形的5个数分别为$n,n-1,n+1,n-7,n+7$,所以$n+(n-1)+(n+1)+(n-7)+(n+7)=65$,解得$n=13$.所以$n-7=13-7=6$,即其中最小的数为6.

9. 定义：C是线段AB($5＜AB＜10$)上的一点,若点C将AB分得的两条线段中,有一条线段的长与AB的长的和是10,则称C是线段AB的“圆满分割点”.已知$MN= 8$,P,Q分别是线段MN,PN的“圆满分割点”,则QN的长是______4或2.

答案： 4或2 提示:由"圆满分割点"的定义,易得$PN=2$或$PM=2$.当$PN=2$时,点$Q$不能满足成为$PN$的"圆满分割点"的前提条件($5＜PN＜10$),故舍去.所以$PM=2$,$PN=6$.所以$QN=4$或$QP=4$.当$QP=4$时,$QN=2$.

10. 如图是一个长、宽、高分别为a,b,c($a＞b＞c$)的长方体纸盒,将此长方体纸盒沿不同的棱剪开,展成各不相同的平面图形,则在这些不同的平面图形中,周长的最大值是______(用含a,b,c的代数式表示).

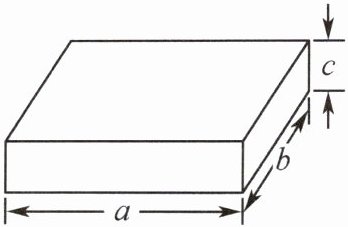
答案：
$8a+4b+2c$ 提示:如图,周长的最大值是$8a+4b+2c$.

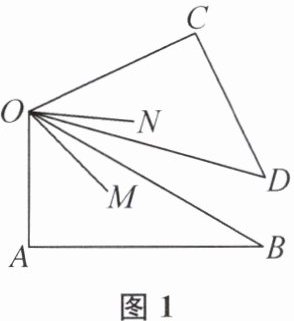
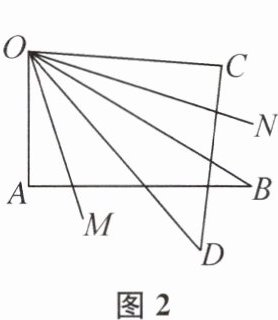
11. (南京市秦淮区期末)一副三角板AOB与COD按如图所示的方式摆放,且$∠A= ∠C= 90^{\circ }$,$∠AOB= 60^{\circ }$,$∠COD= 45^{\circ }$,ON平分$∠COB$,OM平分$∠AOD$.若三角板COD绕点O顺时针旋转(从图1到图2),设图1、图2中$∠NOM$的度数分别为α,β,则$α+β= $______°.


105

答案： 105 提示:如题图1,因为$ON$平分$\angle COB$,$OM$平分$\angle AOD$,所以$\angle NOB=\angle CON=\frac{1}{2}\angle COB=\frac{1}{2}(45^{\circ}+\angle BOD)$,$\angle MOD=\angle MOA=\frac{1}{2}\angle AOD=\frac{1}{2}(60^{\circ}+\angle BOD)$,所以$\angle NOM=\alpha=\angle NOB+\angle MOD-\angle BOD=\frac{1}{2}(45^{\circ}+60^{\circ})$.如题图2,同理,$\angle NOB=\frac{1}{2}\angle COB=\frac{1}{2}(45^{\circ}-\angle BOD)$,$\angle MOD=\frac{1}{2}\angle AOD=\frac{1}{2}(60^{\circ}-\angle BOD)$,所以$\angle NOM=\beta=\angle NOB+\angle MOD+\angle BOD=\frac{1}{2}(45^{\circ}+60^{\circ})$.所以$\alpha+\beta=45^{\circ}+60^{\circ}=105^{\circ}$.