第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
8. 某休闲广场的地面中间是一块正六边形地砖,周围是用正方形和正三角形地砖按如图方式依次向外铺设 10 圈而成,其中第 1 圈有 6 块正方形和 6 块正三角形地砖,则铺设该广场共用地砖
661
块.
答案:
661 提示:根据题意分析可得,从里向外的第1层包括6个正三角形,6个正方形,1个正六边形。第2层包括18个正三角形,6个正方形,此后,每层都比前一层多12个正三角形。依此递推,第10层中含有正三角形6+12×9=114(个)。所以铺设该广场共用地砖6+18+...+114+6×10+1=661(块)。
9. 一个正方体蛋糕竖着切 5 刀,被分成的块数最多为
16
.
答案:
16 提示:当切1刀时,块数为1+1=2;当切2刀时,块数最多为1+1+2=4;当切3刀时,块数最多为1+1+2+3=7……当切n刀时,块数最多为$1+(1+2+3+\cdots+n)=1+\frac{n(n + 1)}{2}$。则切5刀时,块数最多为$1+\frac{5×6}{2}$=16。
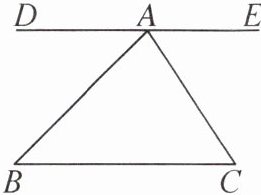
10. 如图,直线 DE 经过点 A,DE//BC,∠B= 48°,∠C= 63°.
(1)∠DAB=
(2)通过求上述三个角的度数,请你说明三角形的内角和为什么是 180°.
(1)∠DAB=
48°
;∠EAC= 63°
;∠BAC= 69°
.(2)通过求上述三个角的度数,请你说明三角形的内角和为什么是 180°.
解:因为DE//BC,所以∠DAB=∠B,∠EAC=∠C。又因为∠DAB+∠BAC+∠EAC=180°,所以∠B+∠BAC+∠C=180°。即三角形的内角和是180°。

答案:
(1)$48^{\circ}$ $63^{\circ}$ $69^{\circ}$ 提示:因为DE//BC,所以∠DAB=∠B,∠EAC=∠C。因为∠B=48°,∠C=63°,所以∠DAB=48°,∠EAC=63°。因为∠DAB+∠BAC+∠EAC=180°,所以∠BAC=180° - 48° - 63°=69°。
(2)解:因为DE//BC,所以∠DAB=∠B,∠EAC=∠C。又因为∠DAB+∠BAC+∠EAC=180°,所以∠B+∠BAC+∠C=180°。即三角形的内角和是180°。
(1)$48^{\circ}$ $63^{\circ}$ $69^{\circ}$ 提示:因为DE//BC,所以∠DAB=∠B,∠EAC=∠C。因为∠B=48°,∠C=63°,所以∠DAB=48°,∠EAC=63°。因为∠DAB+∠BAC+∠EAC=180°,所以∠BAC=180° - 48° - 63°=69°。
(2)解:因为DE//BC,所以∠DAB=∠B,∠EAC=∠C。又因为∠DAB+∠BAC+∠EAC=180°,所以∠B+∠BAC+∠C=180°。即三角形的内角和是180°。
11. 如图,第 1 个多边形由正三角形"扩展"而来,边数记为$a_3= 12,$第 2 个多边形由正方形"扩展"而来,边数记为$a_4= 20……$以此类推,由正 n 边形"扩展"而来的多边形的边数记为aₙ(n≥3),则$a_1₀= $
110
.
答案:
110 提示:根据题意,得$a_{3}=12=3×4=3×(3 + 1)$;$a_{4}=20=4×5=4×(4 + 1)$;$a_{5}=30=5×6=5×(5 + 1)$;…由此发现$a_{n}=n(n + 1)$,所以$a_{10}=10×11=110$。
12. 【问题提出】
连接五边形 ABCDE 的五个顶点和它内部的 n 个点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形,可分得多少个三角形?(不计被分割的三角形)
【问题探究】
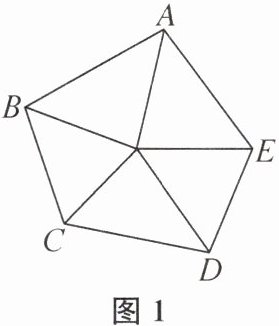
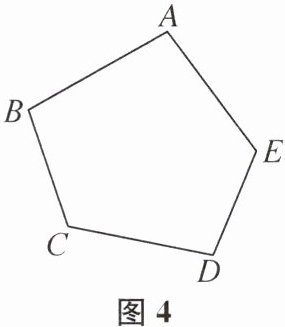
(1)如图 1,当五边形内有 1 个点时,可分得______个三角形.
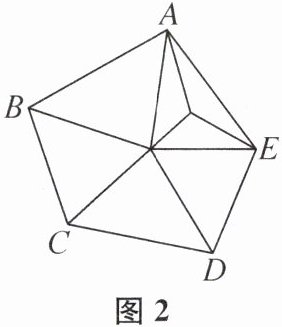
(2)当五边形内有 2 个点时,可分得多少个三角形?我们在图 1 五边形 ABCDE 的内部再添加 1 个点,这个点的位置会有两种情况:可能在图 1 分割成的某个三角形的内部,如图 2 所示;也可能在三角形的某条公共边上,如图 3 所示.显然,不管哪种情况,都可分得______个三角形.
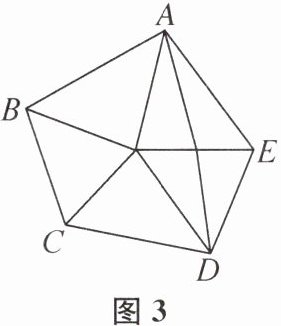
(3)当五边形内有 3 个点时,可分得______个三角形.请在图 4 中画出一种分割示意图.
【问题解决】
(4)连接五边形 ABCDE 的五个顶点和它内部的 n 个点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形,可分得______个三角形.
【拓展延伸】
(5)若连接六边形的六个顶点和它内部的 m 个点,可把六边形区域分割成______个互不重叠的三角形.
连接五边形 ABCDE 的五个顶点和它内部的 n 个点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形,可分得多少个三角形?(不计被分割的三角形)
【问题探究】




(1)如图 1,当五边形内有 1 个点时,可分得______个三角形.
(2)当五边形内有 2 个点时,可分得多少个三角形?我们在图 1 五边形 ABCDE 的内部再添加 1 个点,这个点的位置会有两种情况:可能在图 1 分割成的某个三角形的内部,如图 2 所示;也可能在三角形的某条公共边上,如图 3 所示.显然,不管哪种情况,都可分得______个三角形.
(3)当五边形内有 3 个点时,可分得______个三角形.请在图 4 中画出一种分割示意图.
【问题解决】
(4)连接五边形 ABCDE 的五个顶点和它内部的 n 个点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形,可分得______个三角形.
【拓展延伸】
(5)若连接六边形的六个顶点和它内部的 m 个点,可把六边形区域分割成______个互不重叠的三角形.
答案:
(1)5
(2)7
(3)9 提示:画出图形如下,当五边形内有3个点时,可分得5+2×3 - 2=9(个)三角形。


(4)(2n + 3) 提示:由
(1)可知,当五边形内有1个点时,可分得5+2×1 - 2=5(个)三角形;由
(2)可知,当五边形内有2个点时,可分得5+2×2 - 2=7(个)三角形;由
(3)可知,当五边形内有3个点时,可分得5+2×3 - 2=9(个)三角形……以此类推,当五边形内有n个点时,可分得5+2n - 2=(2n + 3)个三角形。
(5)(2m + 4) 提示:如图3 - 7所示,当六边形内有1个点时,可以分得6+2×1 - 2=6(个)三角形;当六边形内有2个点时,可以分得6+2×2 - 2=8(个)三角形;当六边形内有3个点时,可以分得6+2×3 - 2=10(个)三角形……以此类推,可知当六边形内有m个点时,可分得6+2m - 2=(2m + 4)个三角形。




(1)5
(2)7
(3)9 提示:画出图形如下,当五边形内有3个点时,可分得5+2×3 - 2=9(个)三角形。


(4)(2n + 3) 提示:由
(1)可知,当五边形内有1个点时,可分得5+2×1 - 2=5(个)三角形;由
(2)可知,当五边形内有2个点时,可分得5+2×2 - 2=7(个)三角形;由
(3)可知,当五边形内有3个点时,可分得5+2×3 - 2=9(个)三角形……以此类推,当五边形内有n个点时,可分得5+2n - 2=(2n + 3)个三角形。
(5)(2m + 4) 提示:如图3 - 7所示,当六边形内有1个点时,可以分得6+2×1 - 2=6(个)三角形;当六边形内有2个点时,可以分得6+2×2 - 2=8(个)三角形;当六边形内有3个点时,可以分得6+2×3 - 2=10(个)三角形……以此类推,可知当六边形内有m个点时,可分得6+2m - 2=(2m + 4)个三角形。




查看更多完整答案,请扫码查看


