第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
10. 【阅读理解】我们知道|x|的几何意义是:在数轴上数x对应的点与原点的距离,也就是说,|x|表示在数轴上数x与0对应的点之间的距离.这个结论可以推广为:|m-n|表示在数轴上数m,n对应的点之间的距离.
参考阅读材料,解答下列问题.
(1)数轴上数2和5对应的点之间的距离是______;
(2)数轴上数x和-1对应的点之间的距离是______;
【问题探究】
(3)若数轴上数a对应的点位于-3与5之间,化简:|a+3|+|a-5|;
(4)利用数轴探究,当|a-1|+|a-2|的值最小时,数a的取值范围;
【拓展应用】
(5)请利用【问题探究】中的结论,求出|a-1|+|a-2|+|a-3|的最小值.
参考阅读材料,解答下列问题.
(1)数轴上数2和5对应的点之间的距离是______;
(2)数轴上数x和-1对应的点之间的距离是______;
【问题探究】
(3)若数轴上数a对应的点位于-3与5之间,化简:|a+3|+|a-5|;
(4)利用数轴探究,当|a-1|+|a-2|的值最小时,数a的取值范围;
【拓展应用】
(5)请利用【问题探究】中的结论,求出|a-1|+|a-2|+|a-3|的最小值.
答案:
解:
(1)3
(2)$|x + 1|$
(3)因为$-3 ≤ a ≤ 5$,所以$|a + 3| + |a - 5| = a + 3 + 5 - a = 8$.
(4)①如图 1,当$a < 1$时,$|a - 1| + |a - 2| = AB + AC > 1$;
②如图 2,当$1 ≤ a ≤ 2$时,$|a - 1| + |a - 2| = AB + AC = BC = 1$;
③如图 3,当$a > 2$时,$|a - 1| + |a - 2| = AB + AC > 1$.
所以当$|a - 1| + |a - 2|$取最小值时,数 a 的取值范围是$1 ≤ a ≤ 2$.



(5)$|a - 1| + |a - 2| + |a - 3|$表示在数轴上数 a 对应的点与数 1,2,3 对应的点的距离之和,由
(4)可知,当$1 ≤ a ≤ 3$时,$|a - 1| + |a - 3|$的值最小,又因为$a = 2$时,$|a - 2|$的值最小,所以当$a = 2$时,$|a - 1| + |a - 2| + |a - 3|$取最小值,且最小值为$|2 - 1| + |2 - 2| + |2 - 3| = 1 + 0 + 1 = 2$.
解:
(1)3
(2)$|x + 1|$
(3)因为$-3 ≤ a ≤ 5$,所以$|a + 3| + |a - 5| = a + 3 + 5 - a = 8$.
(4)①如图 1,当$a < 1$时,$|a - 1| + |a - 2| = AB + AC > 1$;
②如图 2,当$1 ≤ a ≤ 2$时,$|a - 1| + |a - 2| = AB + AC = BC = 1$;
③如图 3,当$a > 2$时,$|a - 1| + |a - 2| = AB + AC > 1$.
所以当$|a - 1| + |a - 2|$取最小值时,数 a 的取值范围是$1 ≤ a ≤ 2$.



(5)$|a - 1| + |a - 2| + |a - 3|$表示在数轴上数 a 对应的点与数 1,2,3 对应的点的距离之和,由
(4)可知,当$1 ≤ a ≤ 3$时,$|a - 1| + |a - 3|$的值最小,又因为$a = 2$时,$|a - 2|$的值最小,所以当$a = 2$时,$|a - 1| + |a - 2| + |a - 3|$取最小值,且最小值为$|2 - 1| + |2 - 2| + |2 - 3| = 1 + 0 + 1 = 2$.
11. 对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足2倍的数量关系,则称该点是其他两个点的“联盟点”.
例如:如图,数轴上点A,B,C表示的数分别为1,3,4,此时B是点A,C的“联盟点”.
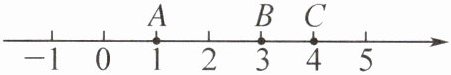
(1)若点A表示的数是-2,点B表示的数是4,点$C_1,C_2,C_3$表示的数分别是3,2,0,则其中是点A,B的“联盟点”的是______.
(2)已知点A表示的数是-10,点B表示的数是30,P为数轴上的一个动点.
①若点P在点B的左侧,且P是点A,B的“联盟点”,求此时点P表示的数;
②若点P在点B的右侧,P,A,B三点中有一个点恰好是其他两个点的“联盟点”,则此时点P表示的数为______.
例如:如图,数轴上点A,B,C表示的数分别为1,3,4,此时B是点A,C的“联盟点”.
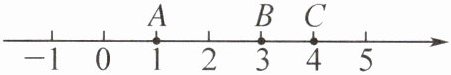
(1)若点A表示的数是-2,点B表示的数是4,点$C_1,C_2,C_3$表示的数分别是3,2,0,则其中是点A,B的“联盟点”的是______.
(2)已知点A表示的数是-10,点B表示的数是30,P为数轴上的一个动点.
①若点P在点B的左侧,且P是点A,B的“联盟点”,求此时点P表示的数;
②若点P在点B的右侧,P,A,B三点中有一个点恰好是其他两个点的“联盟点”,则此时点P表示的数为______.
$C_{2},C_{3}$
-50 或$\frac{10}{3}$或$\frac{50}{3}$
50 或 70 或 110
答案:
解:
(1)$C_{2},C_{3}$
(2)①设点 P 表示的数为 x.
当点 P 在点 A 的左侧时,$30 - x = 2(-10 - x)$,解得$x = -50$,所以点 P 表示的数为 -50;当点 P 在线段 AB 上且离点 A 较近时,$30 - x = 2(x + 10)$,解得$x = \frac{10}{3}$,所以点 P 表示的数为$\frac{10}{3}$;当点 P 在线段 AB 上且离点 B 较近时,$x + 10 = 2(30 - x)$,解得$x = \frac{50}{3}$,所以点 P 表示的数为$\frac{50}{3}$.
综上所述,点 P 表示的数为 -50 或$\frac{10}{3}$或$\frac{50}{3}$.
②50 或 70 或 110 提示:设点 P 表示的数为 x.当 P 为点 A,B 的“联盟点”时,$PA = 2PB$,所以$x + 10 = 2(x - 30)$,解得$x = 70$,即此时点 P 表示的数为 70;当 A 为点 P,B 的“联盟点”时,$PA = 2AB$,所以$x + 10 = 80$,解得$x = 70$,即此时点 P 表示的数为 70;当 B 为点 A,P 的“联盟点”且离点 P 较近时,$AB = 2PB$,所以$40 = 2(x - 30)$,解得$x = 50$,即此时点 P 表示的数为 50;当 B 为点 A,P 的“联盟点”且离点 A 较近时,$PB = 2AB$,所以$x - 30 = 80$,解得$x = 110$,即此时点 P 表示的数为 110.
(1)$C_{2},C_{3}$
(2)①设点 P 表示的数为 x.
当点 P 在点 A 的左侧时,$30 - x = 2(-10 - x)$,解得$x = -50$,所以点 P 表示的数为 -50;当点 P 在线段 AB 上且离点 A 较近时,$30 - x = 2(x + 10)$,解得$x = \frac{10}{3}$,所以点 P 表示的数为$\frac{10}{3}$;当点 P 在线段 AB 上且离点 B 较近时,$x + 10 = 2(30 - x)$,解得$x = \frac{50}{3}$,所以点 P 表示的数为$\frac{50}{3}$.
综上所述,点 P 表示的数为 -50 或$\frac{10}{3}$或$\frac{50}{3}$.
②50 或 70 或 110 提示:设点 P 表示的数为 x.当 P 为点 A,B 的“联盟点”时,$PA = 2PB$,所以$x + 10 = 2(x - 30)$,解得$x = 70$,即此时点 P 表示的数为 70;当 A 为点 P,B 的“联盟点”时,$PA = 2AB$,所以$x + 10 = 80$,解得$x = 70$,即此时点 P 表示的数为 70;当 B 为点 A,P 的“联盟点”且离点 P 较近时,$AB = 2PB$,所以$40 = 2(x - 30)$,解得$x = 50$,即此时点 P 表示的数为 50;当 B 为点 A,P 的“联盟点”且离点 A 较近时,$PB = 2AB$,所以$x - 30 = 80$,解得$x = 110$,即此时点 P 表示的数为 110.
查看更多完整答案,请扫码查看


