《2025年小题狂做七年级数学上册苏科版巅峰版》

10. 如图,P是线段AB上一点,C,D两点同时从点P,B出发分别以1 cm/s和2 cm/s的速度沿线段AB向左运动(点C在线段AP上,点D在线段BP上). 已知点C,D运动到任一时刻时,总有PD= 2AC.
(1)线段AP与线段AB的数量关系是______.
(2)若Q是线段AB上一点,且AQ-BQ= PQ,试说明：AP= PQ.
(3)若点C,D运动5 s后,恰好有CD= 1/2AB,此时点C停止运动,点D在线段PB上继续运动,M,N分别是CD,PD的中点,MN/AB的值是否发生变化？若变化,请说明理由；若不变,请求出MN/AB的值.

答案：

(1)AB=3AP 提示:根据点C,D的运动速度知,BD=2PC.因为PD=2AC,所以BD+PD=2(PC+AC),即PB=2AP.所以AB=3AP.
(2)如图1,根据题意,得AQ＞BQ,所以AQ=AP+PQ.因为AQ-BQ=PQ,所以AQ=BQ+PQ,所以AP=BQ.又由
(1),得AP=$\frac{1}{3}$AB,所以PQ=AB-AP-BQ=$\frac{1}{3}$AB,所以AP=PQ.
(3)$\frac{MN}{AB}$的值不变,值为$\frac{1}{12}$.如图2,当点C停止运动时,有CD=$\frac{1}{2}$AB,所以AC+BD=$\frac{1}{2}$AB,所以AP-PC+BD=$\frac{1}{2}$AB.因为AP=$\frac{1}{3}$AB,PC=5cm,BD=10cm,所以$\frac{1}{3}$AB-5+10=$\frac{1}{2}$AB,解得AB=30cm.因为M是CD的中点,N是PD的中点,所以MN=MD-ND=$\frac{1}{2}$CD-$\frac{1}{2}$PD=$\frac{1}{2}$PC=$\frac{5}{2}$cm,所以$\frac{MN}{AB}$=$\frac{1}{12}$.

11. 如图,射线AB上有一点C,AC= 12,一动点P从点C出发,以每秒m个单位长度的速度沿射线CB的方向运动. 同时,射线CB开始绕点C按顺时针方向以每秒30度的速度旋转一周.
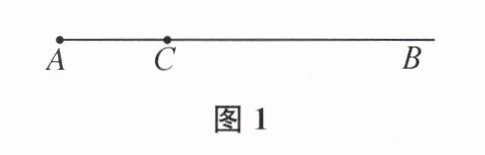
(1)当CB第一次转至与AC垂直时,PC= ______(用含m的代数式表示).
(2)当A,P,C三点中有一个点是另外两个点构成的线段的中点时,求m的值.
(3)如图2,当射线CB绕点C旋转到CB⊥AC时,点P到达射线CB上的点D处,此时,射线DB开始绕点D按顺时针方向以每秒45度的速度一同旋转,旋转一周停止运动,则再经过______s,AC与DB所在直线垂直.

答案：

(1)3m
(2)解:当CB绕点C顺时针旋转180°时,t=$\frac{180}{30}$=6(s).①若P是AC的中点,则PC=$\frac{1}{2}$AC,即6m=$\frac{1}{2}$×12=6,所以m=1;②若A是PC的中点,则PC=2AC,即6m=2×12=24,所以m=4.当CB绕点C顺时针旋转360°时,t=$\frac{360}{30}$=12(s),此时只能C是AP的中点,则PC=AC,即12m=12,所以m=1.综上所述,m=1或4.
(3)$\frac{12}{5}$或$\frac{24}{5}$或$\frac{36}{5}$ 提示:设再经过ts,AC⊥DB.①如图1,∠BDC=180°-45t°,∠ACD=90°-30t°,易得(180°-45t°)+(90°-30t°)=90°,解得t=$\frac{12}{5}$;②如图2,与①同理,可得(45t°-180°)+(30t°-90°)=90°,解得t=$\frac{24}{5}$;③如图3,与①同理,可得(360°-45t°)+(270°-30t°)=90°,解得t=$\frac{36}{5}$.