《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 四边形 ABCD 内部有 1 000 个点,以顶点 A,B,C,D 和这 1 000 个点能把原四边形分割成最多 n 个没有重叠的小三角形,则 n 的值为 (A)
A.2 002
B.2 001
C.2 000
D.1 001

答案： A　提示:有1个点时，内部分割成4个没有重叠的三角形;有2个点时，内部最多分割成4+2=6(个)没有重叠的三角形;那么有3个点时，内部最多分割成4+2×2=8(个)没有重叠的三角形;有4个点时，内部最多分割成4+2×3=10(个)没有重叠的三角形;有n个点时,内部最多分割成4+2×(n - 1)=(2n + 2)个没有重叠的三角形.故n=2×1000+2=2002.

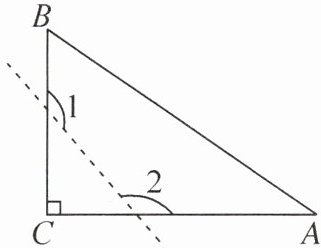
2. 如图,△ABC 为直角三角形,∠C= 90°,沿图中虚线剪去∠C,则∠1+∠2的值为( )


A.315°
B.270°
C.280°
D.156°

答案：
B　提示:如图,因为∠1=180° - ∠3,∠2=180° - ∠4,又因为∠3+∠4=180° - ∠C=90°,所以∠1+∠2=(180° - ∠3)+(180° - ∠4)=360° - (∠3+∠4)=360° - 90°=270°.

3. 连接多边形不相邻的两个顶点的线段叫作多边形的对角线,观察下列图形并阅读相关文字,思考并回答问题:显然,四边形的对角线有 2 条;五边形的对角线有 5 条;对于六边形的对角线条数,光靠"数"数,也能数出来,但已感到较麻烦!需寻找规律!从顶点 A 出发,显然有 3 条对角线,同理,从顶点 B 出发也有 3 条对角线,从每个顶点出发都有 3 条对角线,但从顶点 C 出发,就有重复线段!用此方法算出六边形的对角线条数为 a,且能归纳出 n 边形的对角线条数的计算方法.若一个 n 边形有 35 条对角线,则 a 和 n 的值分别为(C)
A. 12,10 B. 12,12 C. 9,10 D. 9,12

答案： C　提示:从n边形的一个顶点出发有(n - 3)条对角线,n边形有n个顶点，所以共有n(n - 3)条对角线，因为每个顶点都有一条重复的对角线，所以n个顶点共有$\frac{n(n - 3)}{2}$条对角线。故六边形的对角线条数为$\frac{6×(6 - 3)}{2}$=9,即a=9。当n=10时,对角线的条数是$\frac{10×(10 - 3)}{2}$=35;当n=12时，对角线的条数是$\frac{12×(12 - 3)}{2}$=54。综上可知,a和n的值分别为9,10。

4. (泰州市期中)"转化"是数学中的一种重要思想方法,同学们在研究多边形(边数大于 3)的内角和度数时,通常是将多边形的内角和转化为三角形的内角和来解决,从而化陌生的问题为熟悉的情境来解决问题.现从某 n 边形(n＞3)一边上的一点(不包含端点)出发,依次连接多边形的各个顶点,分割得到的所有三角形的内角和是 1 080°,则该 n 边形是 (D)
A.五边形
B.六边形
C.七边形
D.八边形

答案： D　提示:从一个n边形的某个顶点出发作对角线，可以把n边形分为(n - 2)个三角形,所以可列方程(n - 2)×180=1080,解得n=8。则该n边形是八边形。

5. 在同一平面内,我们把两条直线相交将平面分得的区域数记为a_1,三条直线两两相交最多将平面分得的区域数记为a_2,四条直线两两相交最多将平面分得的区域数记为a_3……(n+1)条直线两两相交最多将平面分得的区域数记为aₙ,若$\frac{1}{a_1-1}+\frac{1}{a_2-1}+…+\frac{1}{a_n-1}= \frac{10}{11}$,则 n 的值为 (C)
A.10
B.11
C.20
D.21

答案： C　提示:根据题意，2条直线最多将平面分成4个区域,$a_{1}=4$;3条直线最多将平面分成7个区域,$a_{2}=7$;4条直线最多将平面分成11个区域,$a_{3}=11$;5条直线最多将平面分成16个区域,$a_{4}=16$……则$a_{1}-1=3=1+2$,$a_{2}-1=6=1+2+3$,$a_{3}-1=10=1+2+3+4$,$a_{4}-1=15=1+2+3+4+5$,...,所以$a_{n}-1=1+2+3+4+5+..+(n + 1)=\frac{(n + 1)(n + 2)}{2}$。所以$\frac{1}{a_{1}-1}+\frac{1}{a_{2}-1}+\cdots+\frac{1}{a_{n}-1}=\frac{1}{1+2}+\frac{1}{1+2+3}+\cdots+\frac{1}{1+2+3+\cdots+(n + 1)}=\frac{1}{\frac{(1+2)×2}{2}}+\frac{1}{\frac{(1+3)×3}{2}}+\cdots+\frac{1}{\frac{(1+n + 1)(n + 1)}{2}}=2\left[\frac{1}{2×3}+\frac{1}{3×4}+\cdots+\frac{1}{(n + 1)(n + 2)}\right]=2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{n + 1}-\frac{1}{n + 2}\right)=2\left(\frac{1}{2}-\frac{1}{n + 2}\right)=\frac{n}{n + 2}$。因为$\frac{1}{a_{1}-1}+\frac{1}{a_{2}-1}+\cdots+\frac{1}{a_{n}-1}=\frac{10}{11}$,所以$\frac{n}{n + 2}=\frac{10}{11}$,解得n=20。

6. 中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图,在△ABC 中,分别取 AB,AC 的中点 F,G,连接 FG,过点 A 作 AH⊥FG,垂足为 H.将△ABC 分割后可拼接成长方形 BCDE.若 AH= FG= 4,则△ABC 的面积是32.

答案： 32　提示:因为四边形BCDE是长方形，所以BC=DE,BE=CD。由题意可知,BE=CD=AH=4,DG=HG,EF=HF,所以DG+EF=HG+HF=FG=4。所以BC=DE=4 + 4=8。所以$S_{\triangle ABC}=S_{长方形BCDE}=BC\cdot BE=8×4=32$。

7. 从一个多边形的任何一个顶点出发都只有 5 条对角线,这个多边形的对角线有20条.

答案： 20　提示:设这个多边形的边数是n，由题意，得n - 3=5,解得n=8,所以这个多边形共有对角线$\frac{8×(8 - 3)}{2}$=20(条)。