《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 如图,数轴上三个数从左到右依次是:$-1$,$a-1$,$a$.

只

用

圆

规

在数轴上画出表示数$1-a$的点.下列作图痕迹正确的是(D)

A.
B.
C.
D.

答案： D 提示:因为a-(a-1)=1,所以以-1所对应的点为圆心,a-1与a所对应的两点之间的距离为半径画弧,与数轴上-1所对应的点的右侧的交点即为原点.因为a-1和1-a互为相反数,所以两者表示的点关于原点对称,所以以原点为圆心,a-1所对应的点与原点间的距离为半径画弧,与数轴上-1所对应的点的左侧的交点所表示的数即为1-a,故选项D符合题意.

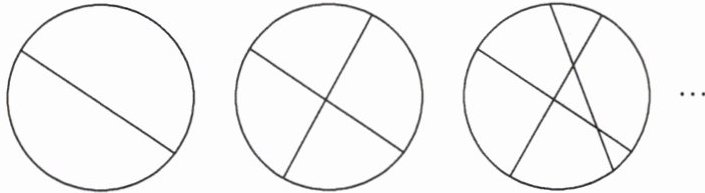
2. 如图,鸡蛋饼的表面可以看作是一个圆面,分割的每一刀都可以抽象为一条直线.切7刀最多可以将鸡蛋饼分成29块.

答案： 29 提示:由题可知,切1刀可将鸡蛋饼分成的块数为2=1+1;切2刀最多可将鸡蛋饼分成的块数为4=1+1+2;切3刀最多可将鸡蛋饼分成的块数为7=1+1+2+3;…,以此类推,切n刀最多可将鸡蛋饼分成的块数为1+1+2+3+…+n=$\frac{n(n+1)}{2}$+1.所以当n=7时,$\frac{n(n+1)}{2}$+1=$\frac{7×8}{2}$+1=29,即切7刀最多可将鸡蛋饼分成29块.

3. 【概念理解】
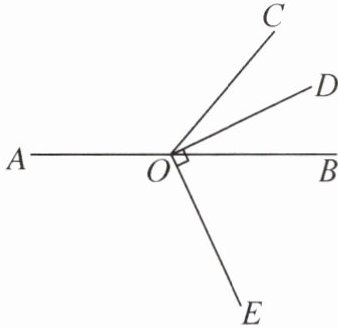
若两个角$\alpha与\beta满足2\alpha+\beta=180^\circ$,则称$\alpha与\beta$互为“准补角”.
(1) 与$50^\circ$角互为“准补角”的角的度数为80或65°.
【初步运用】
(2) 如图,点$O在直线AB$上,射线$OC$,$OD在直线AB$上方($OD在\angle BOC$内部),$OE在直线AB$的右下方,$OE\perp OD$,且$\angle COE= \angle AOE$.判断$\angle COD与\angle AOC$是否互为“准补角”,并说明理由.
【深入探究】
(3) 在(2)的条件下,与$\angle COD$互为“准补角”的角的个数$m随\angle COD$度数的变化而变化,直接写出$\angle COD的度数及对应的m$值.

答案： 解:
(1)80或65
(2)∠COD与∠AOC互为“准补角”.理由如下:
因为∠AOE+∠BOE=180°,∠COE=∠AOE,所以∠COE+∠BOE=180°,所以∠COB+∠BOE=∠COE=180°-∠BOE,所以∠COB=180°-2∠BOE.因为OE⊥OD,所以∠BOD+∠BOE=∠DOE=90°,所以∠BOE=90°-∠BOD.所以∠COB=180°-2(90°-∠BOD)=2∠BOD,所以∠COD=∠BOD.因为∠BOC+∠AOC=180°,所以2∠COD+∠AOC=180°,所以∠COD与∠AOC互为“准补角”.
(3)当∠COD=36°或∠COD=60°时,m=2;当∠COD=45°或∠COD=30°时,m=3;其他情况下,与∠COD互为“准补角”的角只有∠AOC,即m=1. 提示:设∠COD=x°(0＜x＜90),则∠BOC=2x°,∠AOC=(180-2x)°,∠BOD=∠COD=x°,∠BOE=(90-x)°,∠AOE=∠COE=(90+x)°,∠AOD=(180-x)°.可知∠COD+∠BOE=90°,∠AOD+∠COD=180°,所以∠BOE,∠AOD不可能与∠COD互为“准补角”.由
(2)可知,∠COD一直与∠AOC互为“准补角”.
①若2∠COD+∠BOC=180°,即2x+2x=180,解得x=45.此时∠BOC=90°,∠BOD=45°,∠BOE=45°,∠AOE=∠COE=135°,所以此时与∠COD互为“准补角”的角有∠AOC,∠BOC,∠DOE,故m=3.
②若∠COD+2∠BOC=180°,即x+2×2x=180,解得x=36,此时∠BOC=72°,∠BOD=36°,∠BOE=54°,∠AOE=∠COE=126°,所以此时与∠COD互为“准补角”的角有∠AOC,∠BOC,故m=2.
③若2∠COD+∠BOD=180°或∠COD+2∠BOD=180°,则2x+x=180,解得x=60.此时∠BOC=120°,∠BOD=60°,∠BOE=30°,∠AOE=∠COE=150°,所以此时与∠COD互为“准补角”的角有∠AOC,∠BOD,故m=2.
④若2∠COD+∠COE=180°,即2x+90+x=180,解得x=30.此时∠BOC=60°,∠BOD=30°,∠BOE=60°,∠AOE=∠COE=120°,所以此时与∠COD互为“准补角”的角有∠AOC,∠AOE,∠COE,故m=3.
综上所述,与∠COD互为“准补角”的角的个数m随∠COD度数的变化而变化.当∠COD=36°或∠COD=60°时,m=2;当∠COD=45°或∠COD=30°时,m=3;其他情况下,与∠COD互为“准补角”的角只有∠AOC,即m=1.