第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 一家商店以每包a元的价格进了20包甲种茶叶,又以每包b元的价格进了30包乙种茶叶(a<b).如果以每包$\frac{a+b}{2}$元的价格卖出这两种茶叶,则卖完后,这家商店(
A.赚了
B.赔了
C.不赔不赚
D.不能确定赚或赔
B
)A.赚了
B.赔了
C.不赔不赚
D.不能确定赚或赔
答案:
B
2. 已知a表示一个两位数,b表示一个一位数,如果把b放在a的右边组成一个三位数,那么这个三位数可以表示为 (
A.100b+a
B.10a+b
C.a+b
D.100a+b
B
)A.100b+a
B.10a+b
C.a+b
D.100a+b
答案:
B
3.(南京市联合体期末)现有下列关于代数式$-m+1$的值的结论:①$-m+1$的值可能是正数;②$-m+1的值一定比-m$大;③$-m+1$的值一定比1小;④$-m+1$的值随着m的增大而减小.其中所有正确结论的序号是 (
A.①②③
B.②③④
C.①②④
D.①③④
C
)A.①②③
B.②③④
C.①②④
D.①③④
答案:
C 提示:当m=0时,-m+1=1>0,故①符合题意;因为-m+1-(-m)=1>0,所以-m+1>-m,故②符合题意;当m=0时,-m+1=1,故③不符合题意;m越大,-m越小,-m+1越小,故④符合题意.
4.(无锡市锡山区期末)若完全相同的8个小长方形按如图所示的方式放置,形成了一个长、宽分别为m,n的大长方形,则图中阴影部分的周长是 (
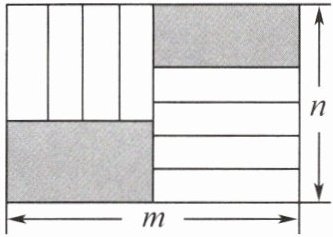
A.4m
B.4n
C.4m+4n
D.8m-8n
B
)
A.4m
B.4n
C.4m+4n
D.8m-8n
答案:
B 提示:设小长方形的长为a,宽为b.根据题意,得m=a+4b,则图中阴影部分的周长为2m+2(n-a)+2(n-4b)=2m+2n-2a+2n-8b=2m+4n-2(a+4b)=2m+4n-2m=4n.
5.(无锡市锡山区期末)如果整式A与整式B的和为一个常数a,那么我们称A,B为常数a的“和谐整式”.例如:$x-6和-x+7$为数1的“和谐整式”.若关于x的整式$9x^{2}-mx+6与-3(3x^{2}-x+m)$为常数k的“和谐整式”(其中m为常数),则k的值为 (
A.3
B.-3
C.5
D.15
B
)A.3
B.-3
C.5
D.15
答案:
B 提示:因为关于x的整式9x²-mx+6与-3(3x²-x+m)为常数k的"和谐整式",所以9x²-mx+6-3(3x²-x+m)=k,即(3-m)x+6-3m=k,无论x取何值都成立,则3-m=0,解得m=3.所以k=6-3m=6-3×3=-3.
6. 已知a与b互为相反数,c与d互为倒数,且$|x|= 1$,则代数式$(2a+b)x-(3cd-bx)+cdx$的值为
-2或-4
.
答案:
-2或-4
7. 若$ab<0$,$ac>0$,$a+c>0$,$|a|<|c|<|b|$,则$|a+b|+|a-c|-|c+b|= $
-2a+2c
.
答案:
-2a+2c 提示:因为ac>0,a+c>0,所以c>0,a>0.又因为ab<0,|a|<|c|<|b|,所以b<0,a<c<-b.所以a+b<0,a-c<0,c+b<0.所以原式=-(a+b)-(a-c)+(c+b)=-a-b-a+c+c+b=-2a+2c.
8. 已知$a_{1},a_{2},a_{3},…,a_{n}$是从1或0中取值的一列数(1和0都至少有一个),若$(a_{1}+2)^{2}+(a_{2}+2)^{2}+(a_{3}+2)^{2}+…+(a_{n}+2)^{2}= 81$,则这列数的个数n为______
14或19
.
答案:
14或19 提示:根据题意,得(1+2)²=9,(0+2)²=4.又因为81是奇数,奇数+偶数=奇数,奇数×奇数=奇数,且数列中1和0都至少有1个,所以这列数中1的个数为奇数且小于9.①若数列中有1个1,则81-9=72,72÷4=18,所以n=18+1=19;②若数列中有3个1,则81-3×9=54,因为54不是4的倍数,所以不合题意,舍去;③若数列中有5个1,则81-5×9=36,36÷4=9,所以n=9+5=14;④若数列中有7个1,则81-7×9=18,因为18不是4的倍数,所以不合题意,舍去.综上所述,个数n的值为14或19.
9. 从古至今,密码的使用在很多方面都发挥着极其重要的作用.有一种密码的明文(真实文),其中的字母按计算机键盘顺序与26个自然数对应(见下表).
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
设明文的任一字母对应的自然数为x,译为密文字母后对应的自然数为$x'$.例如,有一种译码方法按照以下变换实现:$x→x'$,其中$x'是3x+28$被26除所得的余数与1之和($1\leqslant x\leqslant 26$).当$x= 1$时,$x'= 6$,即明文Q译为密文Y;当$x= 10$时,$x'= 7$,即明文P译为密文U.现有某变换,将明文字母对应的自然数x变换为密文字母相应的自然数$x'$:$x→x'$,$x'为3x+b$被26除所得余数与1之和($1\leqslant x\leqslant 26$,$1\leqslant b\leqslant 26$).已知运用此变换,明文H译为密文T,则明文DAY译成密文是______
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
设明文的任一字母对应的自然数为x,译为密文字母后对应的自然数为$x'$.例如,有一种译码方法按照以下变换实现:$x→x'$,其中$x'是3x+28$被26除所得的余数与1之和($1\leqslant x\leqslant 26$).当$x= 1$时,$x'= 6$,即明文Q译为密文Y;当$x= 10$时,$x'= 7$,即明文P译为密文U.现有某变换,将明文字母对应的自然数x变换为密文字母相应的自然数$x'$:$x→x'$,$x'为3x+b$被26除所得余数与1之和($1\leqslant x\leqslant 26$,$1\leqslant b\leqslant 26$).已知运用此变换,明文H译为密文T,则明文DAY译成密文是______
CHQ
.
答案:
CHQ 提示:因为字母H对应的自然数为16,字母T对应的自然数为5,所以由条件得3×16+b被26除后的余数为4.又因为1≤b≤26,所以b=8.当x=13时,3x+8=47,47÷26=1……21,x'=21+1=22,即明文D的密文是C;当x=11时,3x+8=41,41÷26=1……15,x'=15+1=16,即明文A的密文是H;当x=6时,3x+8=26,26÷26=1,x'=0+1=1,即明文Y的密文是Q.综上所述,明文DAY译成密文是CHQ.
查看更多完整答案,请扫码查看


