第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 已知线段 $ AB= 16 $,C,D 是线段 AB 上的两个动点,给出下列结论:①若 C 是 AB 的中点,点 D 在线段 BC 上,$ BD= 3 $,则 $ CD= 5 $;②若 $ AC+BD= \frac{1}{2}CD $,则 $ CD= \frac{32}{3} $;③若 $ CD= 4 $,且 $ AC:BD= 1:2 $,则 $ AC= 4 $;④若 D 是 BC 的中点,$ AC= 6+a(a>0) $,则 $ AC>BD $.其中正确的为( )
A.①③
B.②④
C.①②③
D.①②④
A.①③
B.②④
C.①②③
D.①②④
答案:
D 提示:因为 C 是 AB 的中点,且 AB=16,所以 BC=$\frac{1}{2}$AB=8.因为点 D 在线段 BC 上,且 BD=3,所以 CD=BC - BD=8 - 3=5,故①正确.因为 AC+BD=$\frac{1}{2}$CD,所以点 A,C,D,B 依次排列,所以 AC+CD+BD=AB,所以$\frac{1}{2}$CD+CD=16,所以 CD=$\frac{32}{3}$,故②正确.设 AC=x,则 BD=2x.如图1,当点 C 在点 D 左侧时,AC+CD+BD=AB,即 x+4+2x=16,解得 x=4;如图2,当点 C 在点 D 右侧时,AC+BD - CD=AB,即 x+2x - 4=16,解得 x=$\frac{20}{3}$.综上所述,AC=4 或 AC=$\frac{20}{3}$,故③错误.因为 AC+BC=AB,且 AC=6+a,所以 6+a+BC=16,所以 BC=10 - a.因为 D 是 BC 的中点,所以 BD=$\frac{1}{2}$BC=5 - $\frac{1}{2}$a.因为 AC - BD=6+a - (5 - $\frac{1}{2}$a)=$\frac{3}{2}$a+1>0,所以 AC>BD,故④正确.


D 提示:因为 C 是 AB 的中点,且 AB=16,所以 BC=$\frac{1}{2}$AB=8.因为点 D 在线段 BC 上,且 BD=3,所以 CD=BC - BD=8 - 3=5,故①正确.因为 AC+BD=$\frac{1}{2}$CD,所以点 A,C,D,B 依次排列,所以 AC+CD+BD=AB,所以$\frac{1}{2}$CD+CD=16,所以 CD=$\frac{32}{3}$,故②正确.设 AC=x,则 BD=2x.如图1,当点 C 在点 D 左侧时,AC+CD+BD=AB,即 x+4+2x=16,解得 x=4;如图2,当点 C 在点 D 右侧时,AC+BD - CD=AB,即 x+2x - 4=16,解得 x=$\frac{20}{3}$.综上所述,AC=4 或 AC=$\frac{20}{3}$,故③错误.因为 AC+BC=AB,且 AC=6+a,所以 6+a+BC=16,所以 BC=10 - a.因为 D 是 BC 的中点,所以 BD=$\frac{1}{2}$BC=5 - $\frac{1}{2}$a.因为 AC - BD=6+a - (5 - $\frac{1}{2}$a)=$\frac{3}{2}$a+1>0,所以 AC>BD,故④正确.


2. 用若干黑白两色的正方形按如图所示的方式摆放,依此规律,第 n 个图形中小正方形的总个数是
$(n + 1)^2$[或 n(n + 2)+1]
;若第 n 个图形中白色正方形的个数记为 $ S_{n} $,计算:$ (1+\frac{1}{S_{1}})×(1+\frac{1}{S_{2}})×(1+\frac{1}{S_{3}})×…×(1+\frac{1}{S_{20}})= $$\frac{21}{11}$
.
答案:
$(n + 1)^2$[或 n(n + 2)+1] $\frac{21}{11}$ 提示:由题图可知,第1个图形中小正方形的个数为 3×1+1=4=2²;第2个图形中小正方形的个数为 4×2+1=9=3²;第3个图形中小正方形的个数为 5×3+1=16=4²……以此类推,第 n 个图形中小正方形的个数为 n(n + 2)+1=n²+2n+1=(n + 1)².若第 n 个图形中白色正方形的个数记为$S_n$,则$S_n=n(n + 2)$,$1+\frac{1}{S_n}=\frac{S_n+1}{S_n}=\frac{(n + 1)^2}{n(n + 2)}$,原式=$\frac{2×2}{1×3}×\frac{3×3}{2×4}×\frac{4×4}{3×5}×\frac{5×5}{4×6}×…×\frac{21×21}{20×22}=(\frac{2}{1}×\frac{3}{2}×\frac{4}{3}×…×\frac{21}{20})×(\frac{2}{3}×\frac{3}{4}×\frac{4}{5}×…×\frac{21}{22})=\frac{21}{1}×\frac{2}{22}=\frac{21}{11}$.
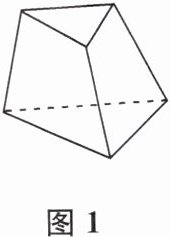
3. 【阅读】
图 1 是小茗同学在课本上看到的一个有趣的几何体.经过查阅资料,得知该几何体的名称叫作三棱台.如图 2,所有的棱台都可以看作是某个棱锥被平行于底面的平面截去一个小的棱锥后得到的几何体.
【探究】
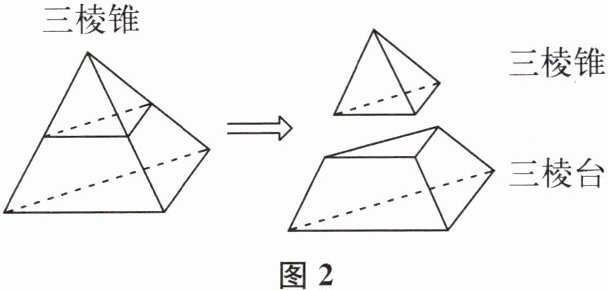
(1) 在图 3 中,用一个平行于四棱锥底面的平面去截这个四棱锥,请画出截得的四棱台的平面直观图.(注意看得见的棱画成实线,看不见的棱画成虚线)

(2) 观察三棱台、四棱台、五棱台的面数(F)、棱数(E)和顶点数(V),分别填入下表中:
| |三棱台|四棱台|五棱台|…|
|面数(F)| | | |…|
|棱数(E)| | | |…|
|顶点数(V)| | | |…|

①小茗通过观察、猜想、验证,发现所有的棱台都满足等式:$ F+E-2V= 2 $,你认为她的结论正确吗?如果正确,请说明理由;如果不正确,请举出反例.
②请你写一条关于 F,E,V 三个量的等式,使其满足棱锥,但是不满足棱台,并说明理由.
图 1 是小茗同学在课本上看到的一个有趣的几何体.经过查阅资料,得知该几何体的名称叫作三棱台.如图 2,所有的棱台都可以看作是某个棱锥被平行于底面的平面截去一个小的棱锥后得到的几何体.

【探究】

(1) 在图 3 中,用一个平行于四棱锥底面的平面去截这个四棱锥,请画出截得的四棱台的平面直观图.(注意看得见的棱画成实线,看不见的棱画成虚线)

(2) 观察三棱台、四棱台、五棱台的面数(F)、棱数(E)和顶点数(V),分别填入下表中:
| |三棱台|四棱台|五棱台|…|
|面数(F)| | | |…|
|棱数(E)| | | |…|
|顶点数(V)| | | |…|

①小茗通过观察、猜想、验证,发现所有的棱台都满足等式:$ F+E-2V= 2 $,你认为她的结论正确吗?如果正确,请说明理由;如果不正确,请举出反例.
②请你写一条关于 F,E,V 三个量的等式,使其满足棱锥,但是不满足棱台,并说明理由.
答案:
解:
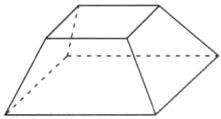
(1) 如图,即为所求.
(2) 填表如下:
三棱台 四棱台 五棱台 ...
面数(F) 5 6 7
棱数(E) 9 12 15 ...
顶点数(V) 6 8 10 ...
①结论正确.理由如下:
结合上表,得三棱台有 2×3=6 个顶点,3×3=9 条棱,3+2=5 个面;四棱台有 2×4=8 个顶点,3×4=12 条棱,4+2=6 个面;五棱台有 2×5=10 个顶点,3×5=15 条棱,5+2=7 个面……以此类推,n 棱台有 2n 个顶点,3n 条棱,(n + 2)个面,故 F+E - 2V=n + 2+3n - 2×2n=2.
②F=V=$\frac{1}{2}$E+1.理由如下:
观察三棱锥、四棱锥、五棱锥的面数(F)、棱数(E)和顶点数(V),如下表所示:
三棱锥 四棱锥 五棱锥 ...
面数(F) 4 5 6 ...
棱数(E) 6 8 10 ...
顶点数(V) 4 5 6 ...
结合上表,得三棱锥有 3+1=4 个顶点,2×3=6 条棱,3+1=4 个面;四棱锥有 4+1=5 个顶点,2×4=8 条棱,4+1=5 个面;五棱锥有 5+1=6 个顶点,2×5=10 条棱,5+1=6 个面……以此类推,n 棱锥有(n + 1)个顶点,2n 条棱,(n + 1)个面,即 F=n + 1,E=2n,V=n + 1,所以 n=F - 1=V - 1=$\frac{1}{2}$E,即 F=V=$\frac{1}{2}$E+1.除此之外,容易发现 n + 1+n + 1 - 2n=2,即 F+V - E=2(满足棱台,不符合题意).
综上所述,满足棱锥,但不满足棱台的等量关系为 F=V=$\frac{1}{2}$E+1.
解:
(1) 如图,即为所求.

(2) 填表如下:
三棱台 四棱台 五棱台 ...
面数(F) 5 6 7
棱数(E) 9 12 15 ...
顶点数(V) 6 8 10 ...
①结论正确.理由如下:
结合上表,得三棱台有 2×3=6 个顶点,3×3=9 条棱,3+2=5 个面;四棱台有 2×4=8 个顶点,3×4=12 条棱,4+2=6 个面;五棱台有 2×5=10 个顶点,3×5=15 条棱,5+2=7 个面……以此类推,n 棱台有 2n 个顶点,3n 条棱,(n + 2)个面,故 F+E - 2V=n + 2+3n - 2×2n=2.
②F=V=$\frac{1}{2}$E+1.理由如下:
观察三棱锥、四棱锥、五棱锥的面数(F)、棱数(E)和顶点数(V),如下表所示:
三棱锥 四棱锥 五棱锥 ...
面数(F) 4 5 6 ...
棱数(E) 6 8 10 ...
顶点数(V) 4 5 6 ...
结合上表,得三棱锥有 3+1=4 个顶点,2×3=6 条棱,3+1=4 个面;四棱锥有 4+1=5 个顶点,2×4=8 条棱,4+1=5 个面;五棱锥有 5+1=6 个顶点,2×5=10 条棱,5+1=6 个面……以此类推,n 棱锥有(n + 1)个顶点,2n 条棱,(n + 1)个面,即 F=n + 1,E=2n,V=n + 1,所以 n=F - 1=V - 1=$\frac{1}{2}$E,即 F=V=$\frac{1}{2}$E+1.除此之外,容易发现 n + 1+n + 1 - 2n=2,即 F+V - E=2(满足棱台,不符合题意).
综上所述,满足棱锥,但不满足棱台的等量关系为 F=V=$\frac{1}{2}$E+1.
查看更多完整答案,请扫码查看


