第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 下列结论正确的是 (
A.直线比射线长
B.经过两点有且只有一条直线
C.过三点一定能作三条直线
D.一条直线就是两条射线
B
)A.直线比射线长
B.经过两点有且只有一条直线
C.过三点一定能作三条直线
D.一条直线就是两条射线
答案:
B
2. 过同一平面内互不重合的三点,能确定的直线条数是
1或3
.
答案:
1或3
3. 已知C为线段AB上一点,AB= 12,AC= 8,D为直线AB上一点,M,N分别是AB,CD的中点. 若MN= 10,则线段AD的长为
16或24
.
答案:
16或24
4. 已知点C在线段AB上$,M_1,N_1$分别为线段AC,CB的中点$,M_2,N_2$分别为线段$M_1C,N_1C$的中点$,M_3,N_3$分别为线段$M_2C,N_2C$的中点$,…,M_2₀_2_5,N_2₀_2_5$分别为线段$M_2₀_2_4C,N_2₀_2_4C$的中点. 若线段AB= a,则线段$M_2₀_2_5N_2₀_2_5$的长是
$\frac{1}{2^{2025}}a$
.
答案:
$\frac{1}{2^{2025}}a$ 提示:因为$M_{1},N_{1}$分别为线段AC,CB的中点,所以$CM_{1}=\frac{1}{2}AC,CN_{1}=\frac{1}{2}BC$,所以$M_{1}N_{1}=\frac{1}{2}AB=\frac{1}{2}a$.同理$M_{2}N_{2}=\frac{1}{2}M_{1}N_{1}=\frac{1}{2}×\frac{1}{2}a=\frac{1}{2^{2}}a,M_{3}N_{3}=\frac{1}{2^{3}}a,\cdots,M_{2025}N_{2025}=\frac{1}{2^{2025}}a$.
5. 已知线段AB= 10,M为AB的中点,线段AB所在直线上有一点P,N为AP的中点. 若MN= 1.5,则AP=
7或13
.
答案:
7或13
6. 已知线段AB= 4,在线段AB的延长线上取一点C,使AC= 5/3 BC,在线段AB的反向延长线上取一点D,使BD= 4/7 DC. 若E为DC的中点,则BE的长是
1
.
答案:
1 提示:因为$AC=\frac{5}{3}BC$,所以$AB+BC=\frac{5}{3}BC$,即$4+BC=\frac{5}{3}BC$,解得$BC=6$.因为$BD=\frac{4}{7}DC$,所以$DC - BC=\frac{4}{7}DC$,解得$DC=14$.又因为E是DC的中点,所以$EC=7$,所以$BE=EC - BC=7 - 6=1$.
7. (苏州市昆山、张家港市期末)已知A,B是数轴上原点两侧的两个点,分别表示整数a,b. 若a+b= -28,且AO= 5BO(O为数轴的原点),则a-b的值等于
-42
.
答案:
-42 提示:因为$AO=5BO$,所以$|a|=5|b|$,又因为点A,B在原点两侧,所以$a=-5b$,所以$-5b + b=-28$,解得$b=7$.所以$a=-35$,所以$a - b=-35 - 7=-42$.
8. (无锡市锡山区期末)如图,C为线段AB的中点,D,E分别为线段AC,BC上的一点,且AD+BE= m,AE+BD= 7/3 m. 若分别用含m的代数式来表示DE与CB的长,则DE=
$\frac{2}{3}m$
,CB=$\frac{5}{6}m$
.
答案:
$\frac{2}{3}m$ $\frac{5}{6}m$ 提示:因为$AE + BD=\frac{7}{3}m$,所以$AD+BE + 2DE=\frac{7}{3}m$.又因为$AD + BE=m$,所以$2DE=\frac{7}{3}m - m=\frac{4}{3}m$,所以$DE=\frac{2}{3}m$.所以$AB=AD + BE+DE=m+\frac{2}{3}m=\frac{5}{3}m$.因为C为线段AB的中点,所以$CB=\frac{1}{2}AB=\frac{5}{6}m$.
9. 已知AB= 10 cm,点C在直线AB上,BC= 4 cm,D是线段AC的中点,求线段BD的长.
下面是马小虎同学的解题过程:
解:根据题意可画出图形,如图所示.
AC= AB+BC= 10+4= 14(cm). 因为D是线段AC的中点,所以DC= 1/2 AC= 7 cm. 所以BD= DC-BC= 3 cm.
若你是老师,会判马小虎满分吗?若会,请说明理由;若不会,请将马小虎的错误指出,并给出你认为正确的解法.
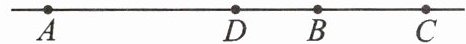
下面是马小虎同学的解题过程:
解:根据题意可画出图形,如图所示.
AC= AB+BC= 10+4= 14(cm). 因为D是线段AC的中点,所以DC= 1/2 AC= 7 cm. 所以BD= DC-BC= 3 cm.
若你是老师,会判马小虎满分吗?若会,请说明理由;若不会,请将马小虎的错误指出,并给出你认为正确的解法.
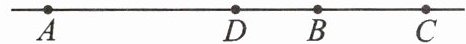
答案:
解:不会判马小虎同学满分,因为需要分两种情况讨论.
①第一种情况同马小虎同学的解题过程一样,可求得$BD = 3$cm.
②第二种情况,根据题意画出图形(如图).

$AC=AB - BC=10 - 4=6$(cm).因为D是线段AC的中点,所以$DC=\frac{1}{2}AC = 3$cm,所以$BD=DC + BC=3 + 4=7$(cm).
综上所述,线段BD的长为3cm或7cm.
解:不会判马小虎同学满分,因为需要分两种情况讨论.
①第一种情况同马小虎同学的解题过程一样,可求得$BD = 3$cm.
②第二种情况,根据题意画出图形(如图).

$AC=AB - BC=10 - 4=6$(cm).因为D是线段AC的中点,所以$DC=\frac{1}{2}AC = 3$cm,所以$BD=DC + BC=3 + 4=7$(cm).
综上所述,线段BD的长为3cm或7cm.
查看更多完整答案,请扫码查看


