第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 下列三个日常现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上,老师测量某个同学的跳远成绩. 其中可以用“两点之间,线段最短”来解释的现象有(
A.①
B.②
C.①③
D.②③
B
)A.①
B.②
C.①③
D.②③
答案:
B
2. a,b,c为同一平面内互不重合的任意三条直线,那么它们的交点个数是( )
A.1或2或3
B.0或1或2或3
C.1或2
D.以上都不对
A.1或2或3
B.0或1或2或3
C.1或2
D.以上都不对
答案:
B 提示:直线a,b,c的位置关系如下图: 由上图可知,平面内三条直线的交点个数可以是0或1或2或3.
由上图可知,平面内三条直线的交点个数可以是0或1或2或3.
B 提示:直线a,b,c的位置关系如下图:
 由上图可知,平面内三条直线的交点个数可以是0或1或2或3.
由上图可知,平面内三条直线的交点个数可以是0或1或2或3. 3. (无锡市期末)如图,点C,D在线段AB上,且AM//NB. 现有下列结论:①若∠AMD= ∠CNB,则∠BDM= ∠ACN;②若∠AMD= ∠CNB,则AN//MB;③若CN//MD,则∠BMD= ∠ANC;④若AN//MB,则∠MAN= ∠MBN. 其中一定正确的是(
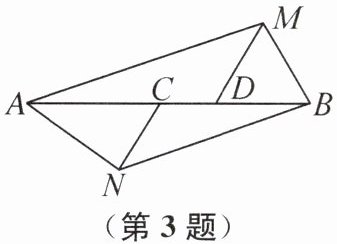
A.①③
B.①④
C.②③
D.②④
B
)
A.①③
B.①④
C.②③
D.②④
答案:
B 提示:因为AM//NB,所以∠MAD=∠ABN.因为∠AMD=∠CNB,所以180°-∠ADM=∠MAD+∠AMD=∠ABN+∠CNB=180°-∠BCN,所以∠BDM=∠ACN,故①正确.由AM//NB,∠AMD=∠CNB不能得出AN//MB,故②不正确.由AM//NB,CN//MD不能得出∠BMD=∠ANC,故③不正确.因为AM//NB,所以∠MAD=∠ABN.因为AN//MB,所以∠NAC=∠MBA.所以∠MAD+∠NAC=∠ABN+∠MBA,所以∠MAN=∠MBN,故④正确.
4. 用一个平面去截正方体(如图),有下列关于截面(截出的面)形状的结论:①可能是三角形;②可能是四边形;③不可能是六边形;④可能是五边形. 其中所有正确结论的序号是(
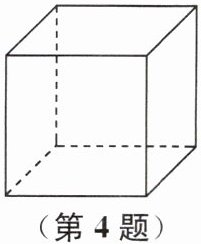
A.①②
B.①④
C.①②④
D.①②③④
C
)
A.①②
B.①④
C.①②④
D.①②③④
答案:
C
5. 将一张正方形纸片ABCD按如图所示的方式折叠,AE,AF为折痕,点B,D折叠后的对应点分别为B',D',有下列结论:①若∠DAF= ∠BAE= 10°,则∠B'AD'= 40°;②若点B'与点D'重合,则∠EAF= 45°;③若∠B'AD'= 10°,则∠EAF= 50°;④若∠EAF= 60°,则∠B'AD'= 30°. 其中正确的是(
A.①③
B.①④
C.②③
D.②④
D
)A.①③
B.①④
C.②③
D.②④
答案:
D 提示:若①中条件成立,则点B'在∠DAD'外部,点D'在∠BAB'外部,此时∠B'AD'=∠DAB-2∠DAF-2∠BAE=50°.若②中条件成立,则∠EAF=∠EAB'+∠FAD'=$\frac{1}{2}$(∠BAB'+∠DAD')=$\frac{1}{2}$×90°=45°.若③中条件成立,会有两种情况:一种是点D'在∠BAB'外,点B'在∠DAD'外,此时∠EAF=∠EAB'+∠B'AD'+∠D'AF=∠B'AD' +$\frac{1}{2}$(∠DAB-∠D'AB')=10°+$\frac{1}{2}$×(90°-10°)=50°;另一种是点D'在∠BAB'内,点B'在∠DAD'内,此时∠EAF=∠FAB'+∠B'AD'+∠D'AE=∠FAD'+∠EAB'-∠B'AD'=∠FAD+∠EAB-∠B'AD'=90°-∠EAF-∠B'AD'=80°-∠EAF,所以∠EAF=40°.若④中条件成立,则∠DAF+∠EAB=30°,所以∠D'AF+∠B'AE=30°<∠EAF,所以∠B'AD'=∠EAF-∠D'AF-∠B'AE=30°.
6. 把一个长16 cm、宽10 cm、高8 cm的长方体表面涂上红漆,然后把它切割成棱长为2 cm的小正方体,则一面涂色的小正方体有
72
块.
答案:
72 提示:因为16÷2=8,10÷2=5,8÷2=4,所以一共可以切成8×5×4=160(块).一面涂色的小正方体有(8-2)×(5-2)×2+(8-2)×(4-2)×2+(5-2)×(4-2)×2=6×3×2+6×2×2+3×2×2=36+24+12=72(块).
7. 如图,已知OM,OA,ON是∠BOC内的三条射线,ON平分∠AOC,OM平分∠BOC,且∠AOB+∠MON= 120°,则∠MON= ______.
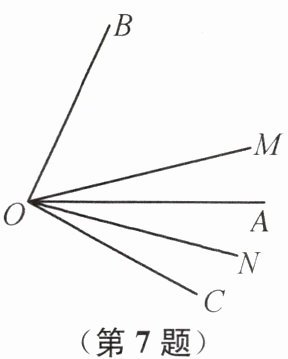

40°
答案:
40° 提示:设∠AOB=x°,∠MON=y°,则∠BOC=∠AOB+∠AOC=x°+∠AOC.因为ON平分∠AOC,OM平分∠BOC,所以∠MOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$x°+$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠AOC,所以∠MON=∠MOC-∠NOC=$\frac{1}{2}$x°,即y=$\frac{1}{2}$x.由题意可知,x+$\frac{1}{2}$x=120,解得x=80.所以∠MON=40°.
8. (宿迁市泗阳县期末)如图,OE⊥AB于点O,OC为∠AOE内的一条射线,点D在CO的延长线上,OF平分∠AOD. 在图中的所有角中,当与∠COE互补的角有且只有两个时,∠COF的度数为______
120°
.
答案:
120° 提示:显然∠DOE与∠COE互补,根据条件另有一角也与∠COE互补.若∠BOF与∠COE互补,则∠DOE=∠BOF,所以∠DOF=∠BOE=90°,而OF平分∠AOD,故∠DOF=∠AOF=90°,此时OC与OA重合,矛盾;若∠DOA与∠COE互补,则由∠DOA与∠COA互补,得∠COE=∠COA=45°,此时∠DOA=135°,从而∠FOA=67.5°,于是∠COF=∠COA+∠FOA=45°+67.5°=112.5°,此时∠BOC=∠BOE+∠COE=135°,也与∠COE互补,矛盾;若∠FOC与∠COE互补,则点E,O,F在同一直线上,而OF平分∠AOD,故OD与OB重合,矛盾;若∠EOF与∠COE互补,则∠DOE=∠EOF,因为OE⊥AB,所以∠BOE=∠AOE=90°,所以∠BOD=∠FOA,又因为OF平分∠AOD,所以∠FOA=∠DOF,所以∠BOD=∠FOA=∠DOF=60°,所以∠COF=∠COA+∠FOA=60°+60°=120°.综上所述,∠COF的度数为120°.
9. 如图,已知∠1+∠ABC= 180°,BE是∠ABC的平分线,若∠E= ∠2,则DF与AB之间有何种位置关系?请说明理由.


答案:
解:DF//AB.理由如下:因为BE是∠ABC的平分线,所以∠2=∠CBE,因为∠E=∠2,所以∠CBE=∠E,所以AE//BC,所以∠A+∠ABC=180°,因为∠1+∠ABC=180°,所以∠A=∠1,所以DF//AB.
查看更多完整答案,请扫码查看


