《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 计算$(-2)^{2025}+3×(-2)^{2024}$的结果是(B)
A.$-2^{2024}$
B.$2^{2024}$
C.$-2^{2025}$
D.$2^{2025}$

答案： B

2. 有理数$a$,$b$在数轴上的位置如图所示,则$a$,$b$,$-a$,$|b|$的大小关系正确的是(A)


A.$|b|＞a＞-a＞b$
B.$|b|＞b＞a＞-a$
C.$a＞|b|＞b＞-a$
D.$a＞|b|＞-a＞b$

答案： A

3. 若$a＞\frac{1}{a}$,则$a$的取值范围是(D)
A.$a＞1$
B.$0＜a＜1$
C.$a＞-1$
D.$-1＜a＜0或a＞1$

答案： D 提示:当a≤-1时,a≤$\frac{1}{a}$,不符合题意;当-1＜a＜0时,a＞$\frac{1}{a}$,符合题意;当0＜a≤1时,a≤$\frac{1}{a}$,不符合题意;当a＞1时,a＞$\frac{1}{a}$,符合题意.综上所述,a的取值范围是-1＜a＜0或a＞1.

4. 在$-2\frac{1}{2},+\frac{7}{10},-3.2,-0.3,3.8,-\frac{\pi}{2}$中,负分数有(C)
A.1个
B.2个
C.3个
D.4个

答案： C

5. 如图,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2025个格子中的数为(B)
A.3
B.-1
C.2
D.-2

答案： B 提示:根据题意,得-2+a+b=a+b+c,所以c=-2.因为b+c+3=c+3+(-1),所以b=-1.因为a+b+c=b+c+3,所以a=3.所以格子中的数按-2,3,-1的规律循环.因为2025÷3=675,所以第2024个格子中的数为-1.

6. 在探究“幻方”、“幻圆”的活动课上,一个小组尝试将数字$-5$,$-4$,$-3$,$-2$,$-1$,0,1,2,3,4,5,6,这12个数填入如图所示的“六角幻星”中,使得6条边上四个数之和都相等,部分数字已填入圆圈中,则$a$的值为(B)
A.4
B.3
C.-3
D.-4

答案： B 提示:因为共有12个数,每一条边上4个数的和都相等,共有六条边,所以每个数都加了两遍,这12个数全部加两遍后和为12,所以每条边的和为2,所以-2,6,2这一条边最后一个圆圈数字应填-4,-5,4,6这一条边最后一个圆圈数字应填-3,-2,4,1这一条边第三个圆圈数字应填-1,此时数字还剩下3,0,5,因为-1,-5这一条边剩下的两个圆圈数字和应为8,即应取3,0,5中的3,5,-3,2这一条边剩下的两个圆圈数字和应为3,即应取3,0,5中的3,0,所以这两条边交汇处a的值应为3.

7. 若$|a-4|+(b-8)^2= 0$,则$\frac{a+b}{ab}$的值为$\frac{3}{8}$.

答案： $\frac{3}{8}$

8. 一列数按如下规律排列：$0,-\frac{3}{5},\frac{4}{5},-\frac{15}{17},\frac{12}{13},-\frac{35}{37},…$.第$n$个数为(-1)$^{n+1}\cdot\frac{n^{2}-1}{n^{2}+1}$.

答案： (-1)$^{n+1}\cdot\frac{n^{2}-1}{n^{2}+1}$

9. 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数：1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长构造正方形,再分别依次从左到右取2个、3个、4个、5个……这样的正方形拼成长方形,如图所示,则序号为⑦的长方形的周长为______.

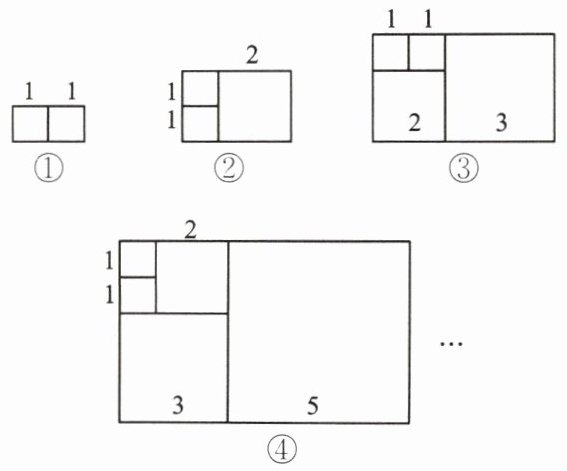
110

答案： 110 提示:由题图可知,序号为①的长方形的宽为1,长为2;序号为②的长方形的宽为2,长为1+2=3;序号为③的长方形的宽为3,长为2+3=5;序号为④的长方形的宽为5,长为3+5=8;序号为⑤的长方形的宽为8,长为5+8=13;序号为⑥的长方形的宽为13,长为8+13=21;序号为⑦的长方形的宽为21,长为13+21=34.所以序号为⑦的长方形的周长为2×(34+21)=110.