第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
10. 某份数学练习限定时间为40 min,学生小明在下午4点后的某一时刻开始答题,此时时针与分针的夹角是$110^{\circ }$.当小明认真思考,做完试题后,发现时间仍是4点多,而此时时针与分针的夹角是$99^{\circ }$,则他比限定时间提前了
2
min做完试题.
答案:
2 提示:设小明于4点x分开始答题,4点y分做完试题,则由条件得120+0.5x-6x=110,6y-120-0.5y=99,解得x=1$\frac{9}{11}$,y=39$\frac{9}{11}$,所以y-x=38<40,所以他比限定时间提前了2 min做完试题.
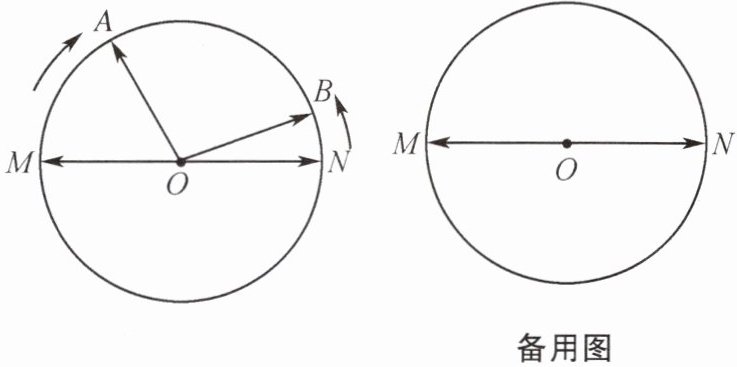
11. 小聪和小明制作了一个模拟钟面.如图,点O为模拟钟面的圆心,点M,O,N在一条直线上,指针OA,OB分别从OM,ON同时出发绕点O转动,OA顺时针转动,OB逆时针转动,OA转动速度为$15^{\circ }/s$,OB转动速度为$5^{\circ }/s$,设转动的时间为t s(t>0),请你试着解决下列问题:
(1)当t= 3时,求$∠AOB$的度数.
(2)当OA与OB第三次重合时,求$∠BOM$的度数.
(3)在OA与OB第四次重合前,当t的值为______时,直线MN平分$∠AOB$.
(3)
(1)当t= 3时,求$∠AOB$的度数.
(2)当OA与OB第三次重合时,求$∠BOM$的度数.
(3)在OA与OB第四次重合前,当t的值为______时,直线MN平分$∠AOB$.

(3)
18或54
答案:
解:
(1)当t=3时,∠AOM=45°,∠BON=15°,所以∠AOB=180°-45°-15°=120°.
(2)当OA与OB第三次重合时,由题意知,15t+5t=360×2+180,解得t=45.所以∠BON=360°-5°×45=135°,∠BOM=180°-135°=45°.
(3)18或54 提示:当OA与OB第四次重合时,15t+5t=360×3+180,解得t=63.当0<t≤12时,OA与OB均在直线MN上方(包含MN),所以直线MN不可能平分∠AOB;当12<t<24时,OA在直线MN下方,OB在直线MN上方,此时∠BON=5t°,∠AON=(15t-180)°,若直线MN平分∠AOB,则有∠BON=∠AON,即15t-180=5t,解得t=18;当24≤t≤36时,OA与OB均在直线MN上方(包含MN),所以直线MN不可能平分∠AOB;当36<t≤48时,OA与OB均在直线MN下方(包含MN),所以直线MN不可能平分∠AOB;当48<t<60时,OA在直线MN上方,OB在直线MN下方,此时∠BON=(360-5t)°,∠AON=(360×2+180-15t)°=(900-15t)°,则有900-15t=360-5t,解得t=54;当60≤t<63时,OA与OB均在直线MN下方(包含MN),所以直线MN不可能平分∠AOB.综上所述,当t=18或t=54时,直线MN平分∠AOB.
(1)当t=3时,∠AOM=45°,∠BON=15°,所以∠AOB=180°-45°-15°=120°.
(2)当OA与OB第三次重合时,由题意知,15t+5t=360×2+180,解得t=45.所以∠BON=360°-5°×45=135°,∠BOM=180°-135°=45°.
(3)18或54 提示:当OA与OB第四次重合时,15t+5t=360×3+180,解得t=63.当0<t≤12时,OA与OB均在直线MN上方(包含MN),所以直线MN不可能平分∠AOB;当12<t<24时,OA在直线MN下方,OB在直线MN上方,此时∠BON=5t°,∠AON=(15t-180)°,若直线MN平分∠AOB,则有∠BON=∠AON,即15t-180=5t,解得t=18;当24≤t≤36时,OA与OB均在直线MN上方(包含MN),所以直线MN不可能平分∠AOB;当36<t≤48时,OA与OB均在直线MN下方(包含MN),所以直线MN不可能平分∠AOB;当48<t<60时,OA在直线MN上方,OB在直线MN下方,此时∠BON=(360-5t)°,∠AON=(360×2+180-15t)°=(900-15t)°,则有900-15t=360-5t,解得t=54;当60≤t<63时,OA与OB均在直线MN下方(包含MN),所以直线MN不可能平分∠AOB.综上所述,当t=18或t=54时,直线MN平分∠AOB.
12. 如图,射线OC在$∠AOB$的内部,且$∠AOB= 72^{\circ }$,若$∠AOB,∠AOC,∠BOC$三个角中,有一个角的度数是另一个角度数的两倍,则$∠AOC$的度数为______
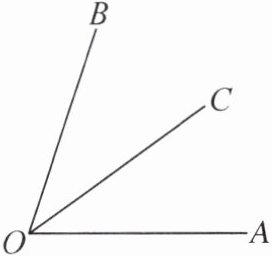
24°或36°或48°
.
答案:
24°或36°或48° 提示:当∠BOC=2∠AOC时,由∠BOC+∠AOC=∠AOB=72°,得∠AOC=24°;当∠AOB=2∠AOC时,∠AOC=$\frac{1}{2}$∠AOB=36°;当∠AOB=2∠BOC时,∠BOC=$\frac{1}{2}$∠AOB=36°,所以∠AOC=36°;当∠AOC=2∠BOC时,由∠BOC+∠AOC=∠AOB=72°,得∠AOC=48°.综上所述,∠AOC的度数为24°或36°或48°.
13. 已知O是直线AB上的一点,$∠COD$是直角,OE平分$∠BOC$.
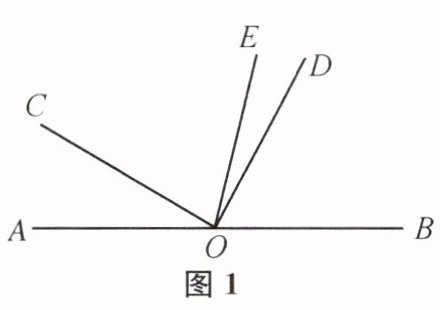
(1)如图1,若$∠AOC= 30^{\circ }$,求$∠DOE$的度数.
(2)如图1,若$∠AOC= α$,请直接写出$∠DOE$的度数(用含α的代数式表示).
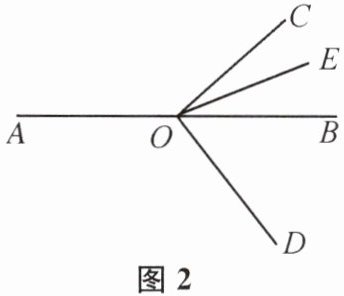
(3)将图1中的$∠DOC$绕顶点O顺时针旋转至图2的位置.
①探究$∠AOC和∠DOE$的度数之间的关系,写出你的结论,并说明理由;
②在$∠AOC$的内部有一条射线OF,满足$∠AOC-4∠AOF= 2∠BOE+∠AOF$,试确定$∠AOF与∠DOE$的度数之间的关系,并说明理由.
(1)如图1,若$∠AOC= 30^{\circ }$,求$∠DOE$的度数.
(2)如图1,若$∠AOC= α$,请直接写出$∠DOE$的度数(用含α的代数式表示).
(3)将图1中的$∠DOC$绕顶点O顺时针旋转至图2的位置.
①探究$∠AOC和∠DOE$的度数之间的关系,写出你的结论,并说明理由;
②在$∠AOC$的内部有一条射线OF,满足$∠AOC-4∠AOF= 2∠BOE+∠AOF$,试确定$∠AOF与∠DOE$的度数之间的关系,并说明理由.


答案:
解:
(1)因为∠AOC=30°,所以∠BOC=180°-30°=150°.因为OE平分∠BOC,所以∠EOC=$\frac{1}{2}$∠BOC=75°.又因为∠COD是直角,所以∠DOE=∠COD-∠EOC=90°-75°=15°.
(2)∠DOE=$\frac{1}{2}$α.
(3)①∠DOE=$\frac{1}{2}$∠AOC.理由如下: 设∠DOE=x,则∠COE=90°-x,∠AOC=180°-2×(90°-x)=2x,所以∠DOE=$\frac{1}{2}$∠AOC. ②4∠DOE-5∠AOF=180°.理由如下: 设∠DOE=x,∠AOF=y,则∠AOC=2x,∠COE=∠BOE=90°-x.因为∠AOC-4∠AOF=2∠BOE+∠AOF,所以2x-4y=2(90°-x)+y,所以4x-5y=180°.即4∠DOE-5∠AOF=180°.
(1)因为∠AOC=30°,所以∠BOC=180°-30°=150°.因为OE平分∠BOC,所以∠EOC=$\frac{1}{2}$∠BOC=75°.又因为∠COD是直角,所以∠DOE=∠COD-∠EOC=90°-75°=15°.
(2)∠DOE=$\frac{1}{2}$α.
(3)①∠DOE=$\frac{1}{2}$∠AOC.理由如下: 设∠DOE=x,则∠COE=90°-x,∠AOC=180°-2×(90°-x)=2x,所以∠DOE=$\frac{1}{2}$∠AOC. ②4∠DOE-5∠AOF=180°.理由如下: 设∠DOE=x,∠AOF=y,则∠AOC=2x,∠COE=∠BOE=90°-x.因为∠AOC-4∠AOF=2∠BOE+∠AOF,所以2x-4y=2(90°-x)+y,所以4x-5y=180°.即4∠DOE-5∠AOF=180°.
查看更多完整答案,请扫码查看


