第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 已知有理数a,b,c在数轴上的位置如图所示,则代数式|a|+|a+b|+|c-a|-|b-c|的值为(
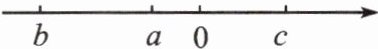
A.-3a
B.2c-a
C.2a-2b
D.b
A
)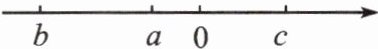
A.-3a
B.2c-a
C.2a-2b
D.b
答案:
A
2. 如果代数式$-2a^2+3b+8$的值为1,那么代数式$-4a^2+6b+2$的值为(
A.12
B.-12
C.16
D.-36
B
)A.12
B.-12
C.16
D.-36
答案:
B 提示:根据题意,得2a²-3b=7,所以-4a²+6b+2=-2(2a²-3b)+2=-2×7+2=-14+2=-12.
3. 已知关于x的方程(a+5b)x-5= 0无解,那么关于x的方程ax-b= 0的解的情况是(
A.有一个解
B.有无数个解
C.有一个解或无数个解
D.无解
C
)A.有一个解
B.有无数个解
C.有一个解或无数个解
D.无解
答案:
C 提示:根据题意,得a+5b=0,即a=-5b.所以当a≠0时,关于x的方程ax-b=0的解为x= b/a = b/(-5b) = -1/5;当a=0时,b=0,关于x的方程ax-b=0有无数个解.
4. 在直线l上取A,B,C三点,使得AB= 5 cm,BC= 3 cm.如果O是线段AC的中点,那么线段OB的长是(
A.2 cm
B.0.5 cm
C.1.5 cm
D.1 cm或4 cm
D
)A.2 cm
B.0.5 cm
C.1.5 cm
D.1 cm或4 cm
答案:
D
5. 定义:若两个角差的绝对值等于60°,则称这两个角互为“优角”.如:∠α= 100°,∠β= 40°,|∠α-∠β|= 60°,则∠α和∠β互为“优角”.如图,已知∠AOB= 120°,射线OC平分∠AOB,∠EOF在∠AOB的内部,若∠EOF= 60°,则图中互为“优角”的共有(
A.6对
B.7对
C.8对
D.9对
B
)A.6对
B.7对
C.8对
D.9对
答案:
B 提示:因为∠AOB=120°,射线OC平分∠AOB,所以∠AOC=∠BOC=1/2∠AOB=60°,所以∠AOB-∠AOC=60°,∠AOB-∠BOC=60°,又因为∠EOF=60°,所以∠AOB-∠EOF=60°,因为∠EOF=∠AOC=60°,所以∠AOF-∠AOE=60°,∠AOF-∠COF=60°,∠BOE-∠EOC=60°,∠BOE-∠BOF=60°,所以图中互为“优角”的共有7对.
6. 如图是某计算机的计算程序,若开始输入x= -1,则最后输出的结果是
-9
.
答案:
-9
7. 一个正方体的每一个面上分别标有数字1,2,3,4,5,6,图1、图2、图3是将该正方体任意摆放后所得的图形,则可推出“?”处的数字是______.
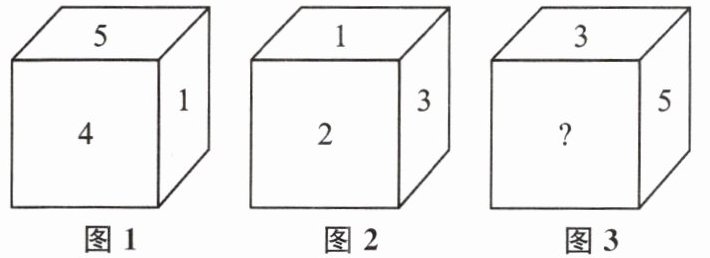

6
答案:
6
8. 已知a,b,c三个数的积为负数,和为正数,且x= $\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{|ab|}{ab}+\frac{|ac|}{ac}+\frac{|bc|}{bc}$,则代数式ax^3+bx^2+cx+1的值为______
1
.
答案:
1
9. 已知有理数a,b,c满足等式|a|+$\frac{3}{4}$= 1-c,|b-1|= c,且c是整数,则式子2a+3b-4c的值为
7/2或5/2
.
答案:
7/2或5/2 提示:任一有理数的绝对值都是非负数,即大于或等于0,所以1-c=|a|+3/4≥0+3/4=3/4,c=|b-1|≥0,所以0≤c≤1/4.又因为c为整数,所以c=0.代入上面两式,分别可得a=1/4或a=-1/4,b=1.当a=1/4,b=1时,原式=2×1/4+3-0=7/2;当a=-1/4,b=1时,原式=2×(-1/4)+3-0=5/2.
10. 在一个圆形时钟的表面,OA表示秒针,OB表示分针(O为两针的旋转中心).若现在时间恰好是12时整,则经过
15 15/59
s,△OAB的面积第一次达到最大.
答案:
15 15/59 提示:当OA⊥OB时,△OAB的面积最大.设经过t s时,OA与OB第一次垂直.又由秒针1 s旋转6°,分针1 s旋转0.1°,可得(6-0.1)t=90,解得t=15 15/59.所以经过15 15/59 s,△OAB的面积第一次达到最大.
11. 如图,在长方形ABCD中,AB= 4 cm,BC= 6 cm,点E在边BC上且BE= 2EC.动点P从点A出发,先以1 cm/s的速度沿A→B运动,然后以2 cm/s的速度沿B→C运动,再以1 cm/s的速度沿C→D运动,最终到达点D.设点P运动的时间是t s,则当t=
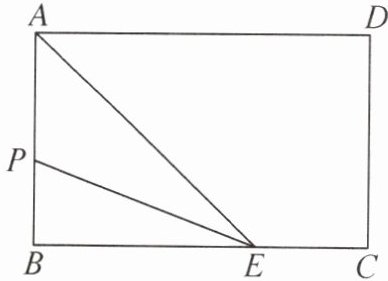
5/2或19/4或15/2
时,△APE的面积等于$5 cm^2.$
答案:
5/2或19/4或15/2 提示:因为BC=6 cm,点E在边BC上且BE=2EC,所以BE=4 cm,EC=2 cm.当点P在边AB上时,0≤t≤4,AP=t cm,所以S△APE=1/2AP·BE=2t(cm²),所以2t=5,解得t=5/2;当点P在线段BE上时,4<t≤6,PE=BE-2(t-4)=4-2t+8=(12-2t)cm,所以S△APE=1/2PE·AB=(24-4t)cm²,所以24-4t=5,解得t=19/4;当点P在线段EC上时,6<t≤7,PE=(t-6)×2=(2t-12)cm,所以S△APE=1/2PE·AB=(4t-24)cm²,所以4t-24=5,解得t=29/4>7,舍去;当点P在边CD上时,7<t≤11,PC=(t-7)cm,所以PD=DC-PC=4-(t-7)=(11-t)cm,所以S△APE=S长方形ABCD-S△ABE-S△ADP-S△EPC=4×6-1/2×4×4-1/2×6(11-t)-1/2×2(t-7)=(2t-10)cm²,所以2t-10=5,解得t=15/2.综上所述,t=5/2或t=19/4或t=15/2.
查看更多完整答案,请扫码查看


