第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
10. 数学上把关于$x的代数式用记号f(x)$来表示.当$x = a$时,代数式的值用$f(a)$表示.例如:代数式$f(x)= x^{2}-x + 1$,当$x = 4$时,代数式的值为$f(4)= 4^{2}-4 + 1= 13$.已知代数式$f(x)= mx^{3}-nx + 3$,若$f(1)= 2024$,则$f(-1)= $
-2018
.
答案:
-2018 提示:因为f
(1)=m-n+3,m-n+3=2024,所以m-n=2021,所以f(-1)=-m+n+3=-(m-n)+3=-2018.
(1)=m-n+3,m-n+3=2024,所以m-n=2021,所以f(-1)=-m+n+3=-(m-n)+3=-2018.
11. 已知在数轴上点A,B,C对应的数分别为a,b,c.
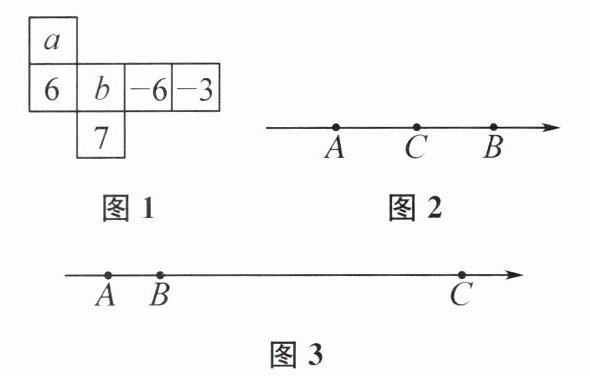
(1)如图1是一个正方体的表面展开图,已知正方体的每一个面都有一个有理数,其相对面上的两个数互为相反数,且在图2中,C为线段AB的中点,则a=
(2)如图3,若a,b,c满足|a + 5|+2|b + 4|+(c - 3)^{2}= 0,①a=

(1)如图1是一个正方体的表面展开图,已知正方体的每一个面都有一个有理数,其相对面上的两个数互为相反数,且在图2中,C为线段AB的中点,则a=
-7
,b= 3
,c= -2
.(2)如图3,若a,b,c满足|a + 5|+2|b + 4|+(c - 3)^{2}= 0,①a=
-5
,b= -4
,c= 3
.②若点A,B沿数轴同时出发向右匀速运动,点A的速度为每秒2个单位长度,点B的速度为每秒1个单位长度.设运动时间为$t\ \unit{s},$在运动过程中,当A为线段BC的中点时,求t的值.当点A与点C重合时,则2t=3-(-5),解得t=4.当点B与点C重合时,则t=3-(-4),解得t=7,可见点A先到达点C,只存在AB=AC,且点A在点B的右侧且在点C的左侧的情况,所以$ \frac{-4+t+3}{2}=-5+2t,$解得t=3.所以当A为线段BC的中点时,t=3.
答案:
(1)-7 3 -2;
(2)①-5 -4 3 提示:因为|a+5|≥0,2|b+4|≥0,(c-3)²≥0,所以a+5=0,b+4=0,c-3=0,所以a=-5,b=-4,c=3.②当点A与点C重合时,则2t=3-(-5),解得t=4.当点B与点C重合时,则t=3-(-4),解得t=7,可见点A先到达点C,只存在AB=AC,且点A在点B的右侧且在点C的左侧的情况,所以 $\frac{-4+t+3}{2}$=-5+2t,解得t=3.所以当A为线段BC的中点时,t=3.
(1)-7 3 -2;
(2)①-5 -4 3 提示:因为|a+5|≥0,2|b+4|≥0,(c-3)²≥0,所以a+5=0,b+4=0,c-3=0,所以a=-5,b=-4,c=3.②当点A与点C重合时,则2t=3-(-5),解得t=4.当点B与点C重合时,则t=3-(-4),解得t=7,可见点A先到达点C,只存在AB=AC,且点A在点B的右侧且在点C的左侧的情况,所以 $\frac{-4+t+3}{2}$=-5+2t,解得t=3.所以当A为线段BC的中点时,t=3.
12. 【原理探究】
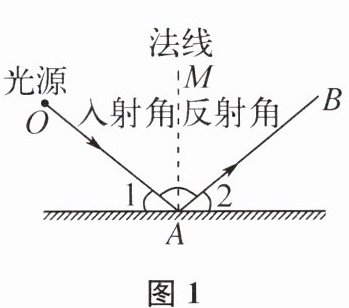
(1)如图1,根据光的反射原理,反射角等于入射角,即反射光线$AB与法线AM的夹角等于入射光线OA与法线AM$的夹角(法线$AM为经过入射点A且与平面镜l$垂直的直线),由此可得$\angle1= \angle2$,理由为 .
【实际应用】
请用【原理探究】获得的结论解决以下问题:
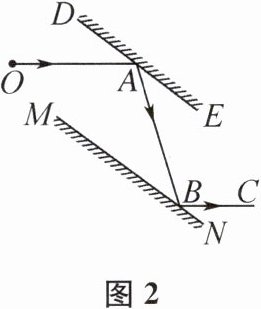
如图2,平面镜$DE$,$MN$相对放置,光线$OA$经过两次反射,$BC$为反射光线.
(2)如果平面镜$DE$,$MN$互相平行,那么入射光线$OA与反射光线BC$平行吗?为什么?
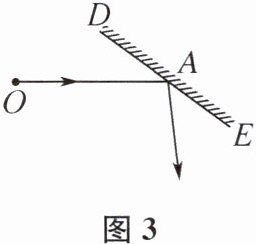
(3)若$\angle OAD = 40^{\circ}$,调整平面镜$MN$的位置,使得$BC// DE$,请在图3中画出相应的平面镜$MN和反射光线BC$,并求此时$\angle ABM$的度数.
(1)如图1,根据光的反射原理,反射角等于入射角,即反射光线$AB与法线AM的夹角等于入射光线OA与法线AM$的夹角(法线$AM为经过入射点A且与平面镜l$垂直的直线),由此可得$\angle1= \angle2$,理由为 .



【实际应用】
请用【原理探究】获得的结论解决以下问题:
如图2,平面镜$DE$,$MN$相对放置,光线$OA$经过两次反射,$BC$为反射光线.
(2)如果平面镜$DE$,$MN$互相平行,那么入射光线$OA与反射光线BC$平行吗?为什么?
(3)若$\angle OAD = 40^{\circ}$,调整平面镜$MN$的位置,使得$BC// DE$,请在图3中画出相应的平面镜$MN和反射光线BC$,并求此时$\angle ABM$的度数.
答案:
(1)等角的余角相等;
(2)入射光线OA与反射光线BC平行.理由如下:同
(1),得∠DAO=∠EAB,∠ABM=∠CBN,所以∠OAB=180°-2∠EAB,∠ABC=180°-2∠ABM.因为DE//MN,所以∠EAB=∠ABM,所以∠OAB=∠ABC,所以OA//BC;
(3)平面镜MN和反射光线BC如图1、图2所示.如图1,当反射光线向右时,延长CB到点F,所以∠FBM=∠CBN,由光的反射原理,得∠EAB=∠OAD=40°,∠ABM=∠CBN=∠FBM,因为BC//DE,所以∠EAB=∠ABF=∠ABM+∠FBM=2∠ABM,因为∠EAB=40°,所以∠ABM=20°,当点M和点N互换位置时,∠ABM=160°;如图2,当反射光线向左时,由光的反射原理,得∠EAB=∠OAD=40°,因为BC//DE,所以∠ABC=∠EAB=40°,易知BF平分∠ABC,∠MBF=∠NBF=90°,所以∠ABF=20°,所以∠ABM=∠ABF+∠MBF=110°,当点M和点N互换位置时,∠ABM=70°.

(1)等角的余角相等;
(2)入射光线OA与反射光线BC平行.理由如下:同
(1),得∠DAO=∠EAB,∠ABM=∠CBN,所以∠OAB=180°-2∠EAB,∠ABC=180°-2∠ABM.因为DE//MN,所以∠EAB=∠ABM,所以∠OAB=∠ABC,所以OA//BC;
(3)平面镜MN和反射光线BC如图1、图2所示.如图1,当反射光线向右时,延长CB到点F,所以∠FBM=∠CBN,由光的反射原理,得∠EAB=∠OAD=40°,∠ABM=∠CBN=∠FBM,因为BC//DE,所以∠EAB=∠ABF=∠ABM+∠FBM=2∠ABM,因为∠EAB=40°,所以∠ABM=20°,当点M和点N互换位置时,∠ABM=160°;如图2,当反射光线向左时,由光的反射原理,得∠EAB=∠OAD=40°,因为BC//DE,所以∠ABC=∠EAB=40°,易知BF平分∠ABC,∠MBF=∠NBF=90°,所以∠ABF=20°,所以∠ABM=∠ABF+∠MBF=110°,当点M和点N互换位置时,∠ABM=70°.


查看更多完整答案,请扫码查看


