《2025年小题狂做七年级数学上册苏科版巅峰版》

9. (扬州市高邮市期末)若一列数$a_{1},a_{2},a_{3},a_{4},...$中的任意三个相邻数之和都是40,且$a_{3}= 3m$,$a_{20}= 16$,$a_{99}= 12-m$,则$a_{2026}= $15.

答案： 15 提示:由题意,可得a₁+a₂+a₃=a₂+a₃+a₄=40,a₂+a₃+a₄=a₃+a₄+a₅=40,a₃+a₄+a₅=a₄+a₅+a₆=40,所以a₁=a₄,a₂=a₅,a₃=a₆.依此类推,可得a₁=a₃ₙ₋₂,a₂=a₃ₙ₋₁,a₃=a₃ₙ(n为正整数).又因为a₃=3m,a₉₉=12-m,99=3×33,所以a₃=a₉₉,即3m=12-m,解得m=3,所以a₃=9.又因为20=3×7-1,所以a₂₀=a₂=16.所以a₁=40-16-9=15.又因为2026=3×676-2,所以a₂₀₂₆=a₁=15.

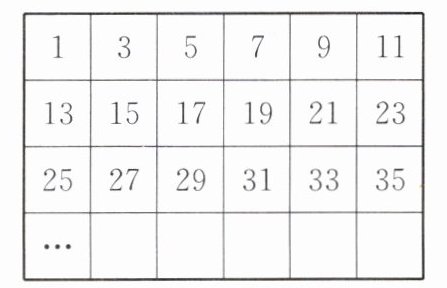
10. 将连续的奇数1,3,5,7,9,…排成如图所示的数表,记$P_{mn}$表示第m行第n个数,如$P_{23}= 17$表示第2行第3个数是17.则$P_{44}= $43,$P_{mn}= $12m+2n-13(用含m,n的代数式表示).

答案： 43 12m+2n-13 提示:观察表格数据,表格中的上下两数相差12,左右两数相差2,因为P₃₄=31,所以P₄₄=P₃₄+12=31+12=43,因为Pₘ₁=12m-11,所以Pₘₙ=12m-11+2(n-1)=12m+2n-13.

11. 如图,点A,B,C,D分别表示四个车站的位置.
(1)用含a,b的代数式表示A,C两站之间的距离是3a-2b.
(2)若已知A,C两站之间的距离是12,求C,D两站之间的距离.
解:CD=(7/2a-2b-1)-(2a-b)=3/2a-b-1.因为3a-2b=12,所以3/2a-b=6,所以CD=6-1=5,即C,D两站之间的距离为5.

答案：
(1)3a-2b
(2)解:CD=(7/2a-2b-1)-(2a-b)=3/2a-b-1.因为3a-2b=12,所以3/2a-b=6,所以CD=6-1=5,即C,D两站之间的距离为5.

12. (无锡市江阴市期末)小敏和小华对一些四位数$\overline{abcd}$(a,b,c,d均为不超过9的正整数)进行了观察、猜想,请帮助他们一起完成探究.
(1)这个四位数可用含a,b,c,d的代数式表示为______1000a+100b+10c+d.
(2)小敏尝试将一些四位数倒排后,再与原数相加,发现和都为11的倍数.
如：1234+4321= 5555= 505×11,4258+8524= 12782= 1162×11.
请仿照小敏的做法再举一个具体例子：______2345+5432=7777=707×11(答案不唯一).
上述结论对于一般的$(\overline{abcd}+\overline{dcba})$也成立吗？请说明理由.
成立.理由如下: 因为$\overline{abcd}+\overline{dcba}=(1000a+100b+10c+d)+(1000d+100c+10b+a)=1001a+110b+110c+1001d=11(91a+91d+10b+10c)$,而91a+91d+10b+10c是正整数,所以$(\overline{abcd}+\overline{dcba})$为11的倍数.
(3)小华认为如果一个四位数的四个数字之和为9的倍数,那么这个四位数也为9的倍数.
如：3231= 359×9,4455= 495×9,6948= 772×9.
请仿照小华的做法再举一个具体例子：______2547=283×9(答案不唯一).
上述结论对于一般的$\overline{abcd}$($a+b+c+d= 9k$,k是整数)也成立吗？请说明理由.
成立.理由如下: 因为$\overline{abcd}=1000a+100b+10c+d=(999a+99b+9c)+(a+b+c+d)=9(111a+11b+c)+9k=9(111a+11b+c+k)$,而111a+11b+c+k是正整数,所以$\overline{abcd}$为9的倍数.

答案：
(1)1000a+100b+10c+d
(2)2345+5432=7777=707×11(答案不唯一) 成立.理由如下: 因为abcd+dcba=(1000a+100b+10c+d)+(1000d+100c+10b+a)=1001a+110b+110c+1001d=11(91a+91d+10b+10c),而91a+91d+10b+10c是正整数,所以(abcd+dcba)为11的倍数.
(3)2547=283×9(答案不唯一) 成立.理由如下: 因为abcd=1000a+100b+10c+d=(999a+99b+9c)+(a+b+c+d)=9(111a+11b+c)+9k=9(111a+11b+c+k),而111a+11b+c+k是正整数,所以abcd为9的倍数.