《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 已知$x＜0,z＞0,xy＞0$,且$|y|＞|z|＞|x|$,那么$|x+z|+|y+z|-|x-y|$的值是(C)
A.正数
B.负数
C.0
D.不能确定符号

答案： C

2. 若$A= -2x^{2}+2x+2$,$B= -3x^{2}+1+2x$,则A与B的大小关系是(A)
A.$A＞B$
B.$A= B$
C.$A＜B$
D.无法确定

答案： A

3. 已知方程$(y^{2}-1)x^{2}+(y+1)x+4= 0$是关于x的一元一次方程. 若$a＞1$,则$|y-a|+|a-x|$的值是(C)
A.3
B.-3
C.$2a+1$
D.$-2a-1$

答案： C

4. 如图,已知$\angle AOB$是直角,$\angle AOC$是锐角,ON平分$\angle AOC$,OM平分$\angle BOC$,则$\angle MON$的度数是(A)
A.$45^{\circ}$
B.$45^{\circ}+\frac{1}{2}\angle AOC$
C.$60^{\circ}-\frac{1}{2}\angle AOC$
D.无法计算

答案： A

5. 观察下列一组图形中点的个数,其中图1中共有4个点,图2中共有10个点,图3中共有19个点……按此规律,则图5中点的个数是(B)
...
A. 31
B. 46
C. 51
D. 66

答案： B

6. 已知$(a+2)^{2}+|b-\frac{1}{2}|= 0$,则代数式$5a^{2}b-[2a^{2}b-(ab^{2}-2a^{2}b)-4]-2ab^{2}$的值为$\frac{13}{2}$.

答案： $\frac{13}{2}$

7. 如图,将三个相同正方形的一个顶点重合放置,且$\angle COE= 40^{\circ}$,$\angle BOF= 30^{\circ}$,则$\angle AOD$的度数为20°.

答案： 20° 提示:因为∠AOF=∠AOB-∠BOF=90°-30°=60°,∠DOE=∠COD-∠COE=90°-40°=50°,所以∠AOD=∠AOF+∠DOE-∠EOF=60°+50°-90°=20°.

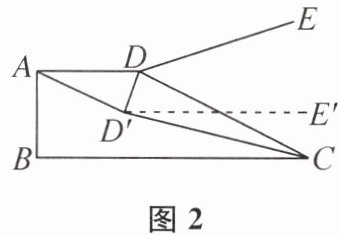
8. 图1是一打孔器的实物图,图2是使用打孔器时的侧面示意图,$AD// BC$,使用打孔器时,AD,DE,DC 分别移动到$AD'$,$D'E'$,$D'C$处.此时$D'E'// BC$,$DD'平分\angle ADC$,若$\angle DD'E'= 62^{\circ}$,则$\angle DCB= $56°.

答案： 56° 提示:因为D'E'//BC,AD//BC,所以AD//D'E',所以∠ADD'=∠DD'E'=62°,因为DD'平分∠ADC,所以∠ADC=2∠ADD'=124°,因为AD//BC,所以∠DCB=180°-∠ADC=56°.

9. 若多项式$2mx^{2}-x^{2}+5x+8-(7x^{2}-3y+5x)$的值与x无关,则代数式$m^{2}-[2m^{2}-(5m-4)+m]$的值为-4.

答案： -4 提示:原多项式=(2m-8)x²+3y+8.因为原多项式的值与x无关,所以2m-8=0,解得m=4.所以m²-[2m²-(5m-4)+m]=-m²+4m-4=-16+16-4=-4.

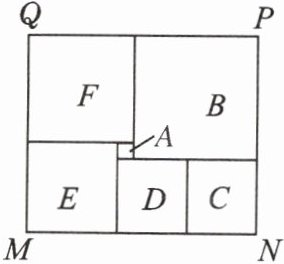
10. 如图,长方形MNPQ是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中$MN= PQ$),正方形四边相等.请根据这个等量关系,计算长方形MNPQ的面积为______.

143

答案： 143 提示:设正方形D和正方形C的边长为x,则由PQ=MN,得2x-1+2x-2=x+1+x+x,解得x=4.所以长方形MNPQ的长为4x-3=13,宽为3x-1=11,所以长方形MNPQ的面积为13×11=143.