《2025年小题狂做七年级数学上册苏科版巅峰版》

1. 已知方程$(m+1)x^{|m|}+3= 0$是关于x的一元一次方程,则$m$的值是 (B)
A.$\pm 1$
B.1
C.$-1$
D.0 或 1

答案： B

2. 整式$mx+2n的值随x$的取值不同而不同,下表是当$x$取不同值时对应的整式的值,则关于$x的方程-mx-2n= 2$的解为 (C)
| $x$ | $-2$ | $-1$ | 0 | 1 | 2 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $mx+2n$ | 2 | 0 | $-2$ | $-4$ | $-6$ |
A.$x= -1$
B.$x= -2$
C.$x= 0$
D.无法计算

答案： C

3. 设$P= 2y-2$,$Q= 2y+3$,且$3P-Q= 1$,则$y$的值是 (B)
A.0.4
B.2.5
C.$-0.4$
D.$-2.5$

答案： B

4. 小李在解方程$5a-x= 13$($x$为未知数)时,误将$-x看作+x$,得方程的解为$x= -2$,那么原方程的解为 (C)
A.$x= -3$
B.$x= 0$
C.$x= 2$
D.$x= 1$

答案： C

5. (苏州市昆山、张家港市期末)如图,“●”“■”“▲”分别表示三种不同的物体,已知前两架天平均保持平衡. 为了使第三架天平也能保持平衡,且在“？”处只放置物体“■”,则应放“■”的个数是 (C)

A.3
B.4
C.5
D.6

答案： C 提示:设物体“●”的质量为x，“■”的质量为y，“▲”的质量为z.由题图，得2x=y+z，x+y=z，所以x=2y，z=3y，所以x+z=2y+3y=5y，所以需要5个“■”.

6. 已知关于$x的一次方程(3a+8)x+7= 0$无解,则$9a^{2}-3a-64$的值为8.

答案： 8 提示:对于方程(3a+8)x+7=0，移项，得(3a+8)x=-7，因为方程(3a+8)x+7=0无解，所以3a+8=0，所以a=-$\frac{8}{3}$，所以9a²-3a-64=9×$(-\frac{8}{3})^2$-3×(-$\frac{8}{3}$)-64=8.

7. 已知$a$,$b$,$c$,$d$为有理数,现规定一种新的运算：$\begin{vmatrix} a&b\\ c&d\end{vmatrix} = ad-bc$. 若$\begin{vmatrix} 2&4\\ 1-x&5\end{vmatrix} = 18$,则$x= $3.

答案： 3

8. 小芳在解关于$x的一元一次方程\frac {4x+K}{5}-\frac {3+2x}{3}= 1$时,发现有一个数模糊不清($K$表示看不清的数),不过小芳翻看了答案,知道这个方程的解是$x= \frac {3}{2}$,于是她很快补好了这个数,则这个数是______9.

答案： 9

9. 按如图所示的程序进行运算,若输出的数为 360,且输入的数$x$不大于 100,则正整数$x$的值为______.

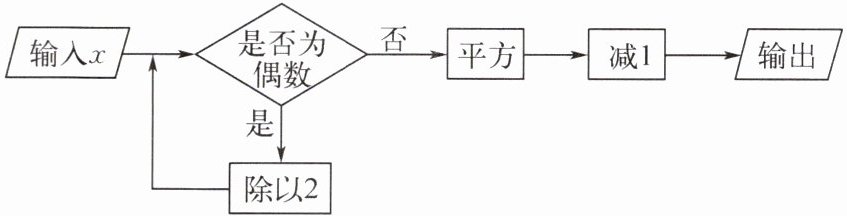
19或38或76

答案： 19或38或76 提示:如果一次运行结果就能输出，则x²-1=360，解得x=19，为正整数，符合题意；如果两次运行结果输出，则$(\frac{1}{2}x)^2$-1=360，解得x=38，为正整数，符合题意；如果三次运行结果输出，则$(\frac{1}{2^2}x)^2$-1=360，解得x=76，符合题意；如果四次运行结果输出，则$(\frac{1}{2^3}x)^2$-1=360，解得x=152＞100，不符合题意.所以若输出结果是360，则正整数x的值为19或38或76.

10. 对于两个不相等的有理数$a$,$b$,规定$\max\{ a,b\}表示a$,$b$中的较大值,例如$\max\{ 2,4\} = 4$. 按照这个规定,方程$\max\{ x,-x\} = 3x+2$的解为______x=-$\frac{1}{2}$.

答案： x=-$\frac{1}{2}$ 提示:由题意可知，x≠0.当x＞-x，即x＞0时，方程变形为x=3x+2，解得x=-1(舍去)；当x＜-x，即x＜0时，方程变形为-x=3x+2，解得x=-$\frac{1}{2}$.综上所述，原方程的解为x=-$\frac{1}{2}$.

11. 已知关于$x的一元一次方程\frac {x}{365}+3= 365x+m的解为x= 2$,则关于$y的一元一次方程\frac {1-y}{365}+365(y-1)= m-3的解为y= $-1.

答案： -1 提示:将关于x的原方程整理，得$\frac{x}{365}$-365x=m-3①，再将关于y的原方程转化为$\frac{1-y}{365}$-365(1-y)=m-3②.将方程②中的1-y看成一个整体，可知方程②与方程①是同一类方程.又由题意可知，方程①的解为x=2，所以1-y=2，所以方程②的解为y=-1.

12. 我们规定：若关于$x的一元一次方程ax= b的解为b+a$,则称该方程为“和解方程”. 例如：方程$2x= -4的解为x= -2$,而$-2= -4+2$,则方程$2x= -4$为“和解方程”.
请根据上述规定,解答下列问题：
(1)已知关于$x的一元一次方程3x= m$是“和解方程”,求$m$的值.
(2)已知关于$x的一元一次方程-2x= mn+n$是“和解方程”,并且它的解是$x= n$,求$m$,$n$的值.

答案：
(1)解方程，得x=$\frac{m}{3}$，所以$\frac{m}{3}$=m+3，解得m=-$\frac{9}{2}$.
(2)根据题意，得-2n=mn+n，且n=mn+n-2，解得n=-$\frac{2}{3}$，m=-3.