第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
10. (镇江市期末)如图,线段AB= 28 cm,点D和点C在线段AB上,且AC∶BC= 5∶2,DC∶AB= 1∶4. 点P从点A出发以4 cm/s的速度沿射线AD向点C运动,点P到达点C所在位置后立即按照原路原速返回,到达点D所在位置后停止运动,点Q从点B出发以1 cm/s的速度沿着射线BC的方向运动,点Q到达点D所在的位置后停止运动. 点P和点Q同时出发,点Q运动的时间为t s.
(1)求线段AD的长.
(2)当C恰好为PQ的中点时,求t的值.
(3)当PQ= 7 cm时,求t的值.

(1)求线段AD的长.
(2)当C恰好为PQ的中点时,求t的值.
(3)当PQ= 7 cm时,求t的值.

答案:
解:
(1)因为$AB = 28$cm,$AC:BC = 5:2$,所以$AC=28×\frac{5}{7}=20$(cm),$BC=28 - 20=8$(cm).因为$DC:AB = 1:4$,所以$DC=28×\frac{1}{4}=7$(cm).所以$AD=AC - DC=20 - 7=13$(cm).
(2)点P从点A运动到点C用时$20÷4 = 5$(s),点P从点A运动到点C,再返回到点D用时$27÷4=\frac{27}{4}$(s),点Q从点B运动到点D用时$15÷1 = 15$(s).所以分三种情况讨论.
①当$0\leqslant t\leqslant5$时,$PC=20 - 4t$,$CQ=8 - t$,所以$20 - 4t=8 - t$,解得$t = 4$;
②当$5<t\leqslant\frac{27}{4}$时,$PC=4t - 20$,$CQ=8 - t$,所以$4t - 20=8 - t$,解得$t=\frac{28}{5}$;
③当$\frac{27}{4}<t\leqslant15$时,$PC=DC = 7$,要想C为PQ中点,则点Q在点C右侧,所以$CQ=8 - t<8-\frac{27}{4}=\frac{5}{4}<7$,所以此种情况不存在.
综上所述,当C恰好为PQ的中点时,t的值是4或$\frac{28}{5}$.
(3)①当$0\leqslant t\leqslant5$时,$PQ=PC + CQ=20 - 4t+8 - t=28 - 5t$,所以$28 - 5t=7$,解得$t=\frac{21}{5}$;
②当$5<t\leqslant\frac{27}{4}$时,$PQ=4t - 20+8 - t=3t - 12$,所以$3t - 12=7$,解得$t=\frac{19}{3}$;
③当$\frac{27}{4}<t\leqslant15$时,因为$PC=DC = 7$cm,所以当点Q运动到点C时,$PQ = 7$cm,此时$t = 8$.
综上所述,当$PQ = 7$cm时,t的值是$\frac{21}{5}$或$\frac{19}{3}$或8.
(1)因为$AB = 28$cm,$AC:BC = 5:2$,所以$AC=28×\frac{5}{7}=20$(cm),$BC=28 - 20=8$(cm).因为$DC:AB = 1:4$,所以$DC=28×\frac{1}{4}=7$(cm).所以$AD=AC - DC=20 - 7=13$(cm).
(2)点P从点A运动到点C用时$20÷4 = 5$(s),点P从点A运动到点C,再返回到点D用时$27÷4=\frac{27}{4}$(s),点Q从点B运动到点D用时$15÷1 = 15$(s).所以分三种情况讨论.
①当$0\leqslant t\leqslant5$时,$PC=20 - 4t$,$CQ=8 - t$,所以$20 - 4t=8 - t$,解得$t = 4$;
②当$5<t\leqslant\frac{27}{4}$时,$PC=4t - 20$,$CQ=8 - t$,所以$4t - 20=8 - t$,解得$t=\frac{28}{5}$;
③当$\frac{27}{4}<t\leqslant15$时,$PC=DC = 7$,要想C为PQ中点,则点Q在点C右侧,所以$CQ=8 - t<8-\frac{27}{4}=\frac{5}{4}<7$,所以此种情况不存在.
综上所述,当C恰好为PQ的中点时,t的值是4或$\frac{28}{5}$.
(3)①当$0\leqslant t\leqslant5$时,$PQ=PC + CQ=20 - 4t+8 - t=28 - 5t$,所以$28 - 5t=7$,解得$t=\frac{21}{5}$;
②当$5<t\leqslant\frac{27}{4}$时,$PQ=4t - 20+8 - t=3t - 12$,所以$3t - 12=7$,解得$t=\frac{19}{3}$;
③当$\frac{27}{4}<t\leqslant15$时,因为$PC=DC = 7$cm,所以当点Q运动到点C时,$PQ = 7$cm,此时$t = 8$.
综上所述,当$PQ = 7$cm时,t的值是$\frac{21}{5}$或$\frac{19}{3}$或8.
11. 已知C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点,则EF/AB= ______. 若AB= 16CF,则AC/BC= ______.
答案:
$\frac{1}{4}$ $\frac{5}{3}$或$\frac{3}{5}$ 提示:因为D为AC的中点,E为BC的中点,所以$AD=DC=\frac{1}{2}AC$,$CE=\frac{1}{2}BC$,所以$DE=DC + CE=\frac{1}{2}(AC + BC)=\frac{1}{2}AB$,因为F为DE的中点,所以$DF=EF=\frac{1}{2}DE=\frac{1}{2}×\frac{1}{2}AB=\frac{1}{4}AB$,所以$\frac{EF}{AB}=\frac{1}{4}$.
①如图1,当$AC>BC$时,易知$AD=DC=\frac{1}{2}AC>\frac{1}{4}AB$,所以$AF=AD + DF=\frac{1}{2}AC+\frac{1}{4}AB<AC$,所以点F在点C左侧,因为$AB=16CF$,所以$DF=\frac{1}{4}AB = 4CF$,所以$CF=DC - DF=\frac{1}{2}AC - 4CF$,所以$AC=10CF$,所以$BC=AB - AC=16CF - 10CF=6CF$,所以$\frac{AC}{CB}=\frac{10CF}{6CF}=\frac{5}{3}$.
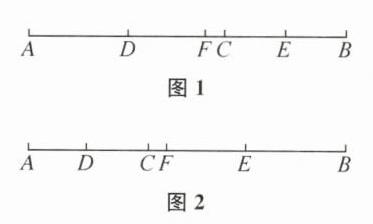
②如图2,当$AC<BC$时,同理可得点F在点C右侧,所以$CF=DF - DC=4CF-\frac{1}{2}AC$,所以$AC=6CF$,所以$BC=AB - AC=16CF - 6CF=10CF$,$\frac{AC}{CB}=\frac{6CF}{10CF}=\frac{3}{5}$.
综上所述,$\frac{AC}{CB}$的值为$\frac{5}{3}$或$\frac{3}{5}$.
$\frac{1}{4}$ $\frac{5}{3}$或$\frac{3}{5}$ 提示:因为D为AC的中点,E为BC的中点,所以$AD=DC=\frac{1}{2}AC$,$CE=\frac{1}{2}BC$,所以$DE=DC + CE=\frac{1}{2}(AC + BC)=\frac{1}{2}AB$,因为F为DE的中点,所以$DF=EF=\frac{1}{2}DE=\frac{1}{2}×\frac{1}{2}AB=\frac{1}{4}AB$,所以$\frac{EF}{AB}=\frac{1}{4}$.
①如图1,当$AC>BC$时,易知$AD=DC=\frac{1}{2}AC>\frac{1}{4}AB$,所以$AF=AD + DF=\frac{1}{2}AC+\frac{1}{4}AB<AC$,所以点F在点C左侧,因为$AB=16CF$,所以$DF=\frac{1}{4}AB = 4CF$,所以$CF=DC - DF=\frac{1}{2}AC - 4CF$,所以$AC=10CF$,所以$BC=AB - AC=16CF - 10CF=6CF$,所以$\frac{AC}{CB}=\frac{10CF}{6CF}=\frac{5}{3}$.

②如图2,当$AC<BC$时,同理可得点F在点C右侧,所以$CF=DF - DC=4CF-\frac{1}{2}AC$,所以$AC=6CF$,所以$BC=AB - AC=16CF - 6CF=10CF$,$\frac{AC}{CB}=\frac{6CF}{10CF}=\frac{3}{5}$.
综上所述,$\frac{AC}{CB}$的值为$\frac{5}{3}$或$\frac{3}{5}$.
12. 如图,在数轴上,点A表示的数是-10,点B表示的数是6.
(1)A,B两点之间的距离为
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,若在数轴上找一点C,使AC= 3BC,则点C表示的数是
(3)若在原点O的左边2个单位长度处放一挡板,一小球P从点A处以每秒4个单位长度的速度向右运动,同时另一小球Q从点B处以每秒2个单位长度的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为t s.
①当t≤4时,请用含t的整式来表示两小球之间的距离PQ的长.
②是否存在这样的t值,使得3BQ + PQ是定值?若存在,求出这样的t与定值;若不存在,请说明理由.
(1)A,B两点之间的距离为
16
.(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,若在数轴上找一点C,使AC= 3BC,则点C表示的数是
2或14
.(3)若在原点O的左边2个单位长度处放一挡板,一小球P从点A处以每秒4个单位长度的速度向右运动,同时另一小球Q从点B处以每秒2个单位长度的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为t s.
①当t≤4时,请用含t的整式来表示两小球之间的距离PQ的长.
当$t\leqslant4$时,$PQ=\begin{cases}16 - 6t(0\leqslant t\leqslant2),\\2t(2<t\leqslant4).\end{cases}$
②是否存在这样的t值,使得3BQ + PQ是定值?若存在,求出这样的t与定值;若不存在,请说明理由.
存在.当$0\leqslant t\leqslant2$或$4\leqslant t\leqslant8$时,$3BQ+PQ$是定值,定值分别为16,32.
答案:
(1)16
(2)2或14 提示:设点C表示的数是x,则$AC=|x - (-10)|=|x + 10|$,$BC=|x - 6|$.当点C在线段AB上时,$AC=x + 10$,$BC=6 - x$,由$AC=3BC$,得$x + 10=3(6 - x)$,解得$x=2$;当点C在线段AB的延长线上时,$AC=x + 10$,$BC=x - 6$,由$AC=3BC$,得$x + 10=3(x - 6)$,解得$x=14$.综上所述,满足题意的点C所表示的数是2或14.
(3)解:①由条件,得小球P碰到挡板的时间为$[(-2)-(-10)]÷4 = 2$(s),小球Q碰到挡板的时间为$[6-(-2)]÷2 = 4$(s).
当$0\leqslant t\leqslant2$时,$PQ=16-(4t + 2t)=16 - 6t$;当$2<t\leqslant4$时,$PQ=4t - 8+8 - 2t=2t$.综上所述,当$t\leqslant4$时,$PQ=\begin{cases}16 - 6t(0\leqslant t\leqslant2),\\2t(2<t\leqslant4).\end{cases}$
②存在.当$0\leqslant t\leqslant2$时,$PQ=16 - 6t$,$BQ=2t$,则$3BQ+PQ=6t + 16 - 6t=16$,是定值;
当$2<t<4$时,$PQ=2t$,$BQ=2t$,则$3BQ+PQ=6t + 2t=8t$,不是定值;
当$4\leqslant t\leqslant8$时,$BQ=16 - 2t$,$PQ=4t - 8+2t - 8=6t - 16$,则$3BQ+PQ=48 - 6t+6t - 16=32$,是定值;
当$t>8$时,$BQ=2t - 16$,$PQ=6t - 16$,则$3BQ+PQ=6t - 48+6t - 16=12t - 64$,不是定值.
综上所述,当$0\leqslant t\leqslant2$或$4\leqslant t\leqslant8$时,$3BQ+PQ$是定值,定值分别为16,32.
(1)16
(2)2或14 提示:设点C表示的数是x,则$AC=|x - (-10)|=|x + 10|$,$BC=|x - 6|$.当点C在线段AB上时,$AC=x + 10$,$BC=6 - x$,由$AC=3BC$,得$x + 10=3(6 - x)$,解得$x=2$;当点C在线段AB的延长线上时,$AC=x + 10$,$BC=x - 6$,由$AC=3BC$,得$x + 10=3(x - 6)$,解得$x=14$.综上所述,满足题意的点C所表示的数是2或14.
(3)解:①由条件,得小球P碰到挡板的时间为$[(-2)-(-10)]÷4 = 2$(s),小球Q碰到挡板的时间为$[6-(-2)]÷2 = 4$(s).
当$0\leqslant t\leqslant2$时,$PQ=16-(4t + 2t)=16 - 6t$;当$2<t\leqslant4$时,$PQ=4t - 8+8 - 2t=2t$.综上所述,当$t\leqslant4$时,$PQ=\begin{cases}16 - 6t(0\leqslant t\leqslant2),\\2t(2<t\leqslant4).\end{cases}$
②存在.当$0\leqslant t\leqslant2$时,$PQ=16 - 6t$,$BQ=2t$,则$3BQ+PQ=6t + 16 - 6t=16$,是定值;
当$2<t<4$时,$PQ=2t$,$BQ=2t$,则$3BQ+PQ=6t + 2t=8t$,不是定值;
当$4\leqslant t\leqslant8$时,$BQ=16 - 2t$,$PQ=4t - 8+2t - 8=6t - 16$,则$3BQ+PQ=48 - 6t+6t - 16=32$,是定值;
当$t>8$时,$BQ=2t - 16$,$PQ=6t - 16$,则$3BQ+PQ=6t - 48+6t - 16=12t - 64$,不是定值.
综上所述,当$0\leqslant t\leqslant2$或$4\leqslant t\leqslant8$时,$3BQ+PQ$是定值,定值分别为16,32.
查看更多完整答案,请扫码查看


