《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

12. 如图,将一块正方形空地划出部分区域进行绿化,原正方形空地一边减少了5m,另一边减少了6m,剩余一块面积为$20m^2$的矩形空地,则原正方形空地的边长是10m.

答案： 10

13. 如图,在长为16m,宽为10m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为整个矩形面积的$\frac{7}{10},$则道路的宽为2m.

答案： 2

14. 某种花卉每盆的盈利与每盆的株数有一定的关系:每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元.要使每盆的盈利达到15元,且尽可能地减少成本,则每盆应多植2株.

答案： 2

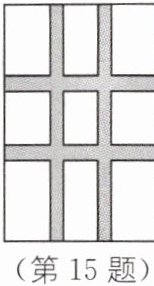
15. 如图,要设计一个长为15cm,宽为10cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度之比为5:4,若要使所有彩条所占面积是原来矩形图案面积的三分之一,应如何设计每个彩条的宽度?

答案： 设每个横彩条的宽度为5x cm,则每个竖彩条的宽度为4x cm,依题意,得(15-2×5x)(10-2×4x)=15×10×(1-$\frac{1}{3}$),整理,得8x²-22x+5=0,解得x₁=$\frac{5}{2}$,x₂=$\frac{1}{4}$.当x=$\frac{5}{2}$时,10-2×4x=-10＜0,不符合题意,舍去;当x=$\frac{1}{4}$时,10-2×4x=8＞0,符合题意,
∴5x=$\frac{5}{4}$,4x=1.故设计每个横彩条的宽度为$\frac{5}{4}$cm,每个竖彩条的宽度为1 cm.

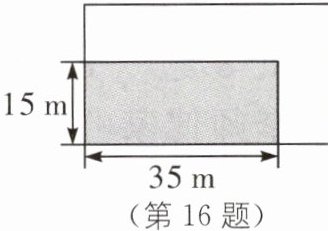
16. 如图,某小区矩形绿地的长,宽分别为35m,15m.现计划对其进行扩充,将绿地的长,宽增加相同的长度后,得到一个新的矩形绿地.
(1)若扩充后的矩形绿地面积为$800m^2,$求新的矩形绿地的长与宽;
(2)若扩充后,实地测量发现新的矩形绿地的长宽之比为5:3.求新的矩形绿地面积.

答案：
(1)设将绿地的长,宽增加x m,则新的矩形绿地的长为(35+x)m,宽为(15+x)m,根据题意,得(35+x)(15+x)=800,整理,得x²+50x-275=0,解得x₁=5,x₂=-55(不符合题意,舍去),
∴35+x=35+5=40,15+x=15+5=20.故新的矩形绿地的长为40 m,宽为20 m.
(2)设将绿地的长,宽增加y m,则新的矩形绿地的长为(35+y)m,宽为(15+y)m,根据题意,得(35+y):(15+y)=5:3,即3(35+y)=5(15+y),解得y=15,
∴(35+y)(15+y)=(35+15)×(15+15)=1500.故新的矩形绿地面积为1500 m².

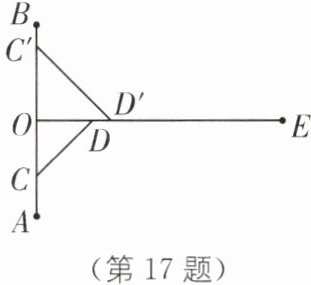
17. 如图,一根木棍OE垂直平分柱子AB,AB= 200cm,OE= 260cm,一只小猫C由柱子底端点A以2cm/s的速度向顶端点B爬行,同时,另一只小猫D由点O以3cm/s的速度沿木棍OE爬行.问:是否存在这样的时刻,使两只小猫与点O组成的三角形面积是$1800cm^2?$

答案： 存在.理由如下:①当小猫C在AO上运动时,设x s时两只小猫与点O组成的三角形面积为1800 cm²,由题意,得$\frac{1}{2}$×3x×(100-2x)=1800,整理,得x²-50x+600=0,解得x₁=20,x₂=30;②当小猫C在OB上运动时,设y s时两只小猫与点O组成的三角形面积为1800 cm²,由题意,得$\frac{1}{2}$×3y(2y-100)=1800,整理,得y²-50y-600=0,解得y₁=60,y₂=-10(舍去).综上所述,在20 s,30 s或60 s时,两只小猫与点O组成的三角形面积是1800 cm².