《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

10. 如图,若$\angle AOB= 45^{\circ}$,$P是\angle AOB$内一点,分别作点$P关于直线OA$,$OB的对称点P_1$,$P_2$,连接$OP_1$,$OP_2$,则下列结论正确的是(D).

A.$OP_1\perp OP_2$,$OP_1\neq OP_2$
B.$OP_1= OP_2$,$OP_1与OP_2$不垂直
C.$OP_1\neq OP_2且OP_1与OP_2$不垂直
D.$OP_1\perp OP_2且OP_1= OP_2$

答案： D

11. 如图,在$\triangle ABC$中,$AB= AC$,$AD\perp BC于点D$,若$AB= 6$,$CD= 4$,则$\triangle ABC$的周长是20.

答案： 20

12. 如图,$\triangle ABC与\triangle A'B'C'关于直线l$对称,$\angle C'= 30^{\circ}$,$\angle B= 90^{\circ}$,则$\angle A$的度数为______.

60°

答案： 60°

13. 下列说法中,正确的有②③④.(把所有正确的答案都写上)
①圆、线段、角、梯形、平行四边形都是轴对称图形；
②若两图形成轴对称,则对称轴两侧的对应点所连成的线段被对称轴垂直平分；
③如果三角形中有两边上的高相等,那么这个三角形一定是等腰三角形；
④等腰三角形顶角的外角平分线与底边平行；
⑤若等腰三角形的一个内角为$80^{\circ}$,则另外两个内角必然都是$50^{\circ}$.

答案： ②③④

14. 如图,点$P为\angle AOB$内一点,分别作出点$P关于OA$,$OB的对称点P_1$,$P_2$,连接$P_1P_2交OA于点M$,交$OB于点N$,$P_1P_2= 15$,则$\triangle PMN$的周长为15.

答案： 15

15. 如图,是屋架设计图的一部分,点$D是斜梁AB$的中点,立柱$BC$,$DE垂直于横梁AC$,$AB= 8m$,$\angle A= 30^{\circ}$,则$DE$长为______2m.

答案： 2m

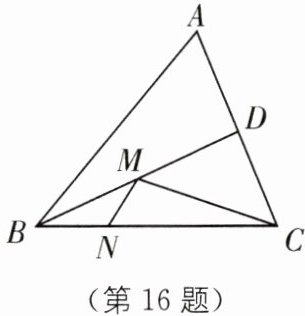
16. 如图,在锐角三角形$ABC$中,$AB= 4$,$\triangle ABC$的面积为8,$BD平分\angle ABC$. 若$M$,$N分别是BD$,$BC$上的动点,则$CM+MN$的最小值是______4.

答案： 4

17. 小明从前面的镜子里看到后面墙上挂钟的时间为$2:30$,则实际时间是9:30.

答案： 9:30

18. 如图,有一张矩形纸条$ABCD$,$AB= 5cm$,$BC= 2cm$,点$M$,$N分别在边AB$,$CD$上,$CN= 1cm$. 现将四边形$BCNM沿MN$折叠,使点$B$,$C分别落在点B'$,$C'$上,当点$B'恰好落在边CD$上时,线段$BM$的长为______$cm$；在点$M从点A运动到点B$的过程中,若边$MB'与边CD交于点E$,则点$E$相应运动的路径长为______$cm$.

答案：
$\sqrt{5}(\sqrt{5}-\frac{3}{2})$　[解析]本题考查与矩形的折叠有关的计算，解答本题需要利用折叠的性质、矩形的性质、解直角三角形等知识
　　如图
(1),
∵四边形ABCD是矩形,
　
∴AB//CD.
　
∴∠1=∠3.
　　由翻折的性质可知∠1=∠2,BM=MB',
　
∴∠2=∠3.
　
∴MB'=NB',
　
∵NB'=$\sqrt{B'C'^2+NC'^2}$=$\sqrt{2^2+1^2}$=$\sqrt{5}$(cm),
　
∴BM=NB'=$\sqrt{5}$cm.
　　　　　　
　　如图
(2),当点M与A重合时,易知AE=EN,设
AE=EN=xcm,
　　　　　　
　　在Rt△ADE中,则有$x^2=2^2+(4-x)^2$,
　　解得$x=\frac{5}{2}$,
∴DE=$4-\frac{5}{2}=\frac{3}{2}$(cm).
　　如图
(3),当点M运动到MB'⊥AB时，DE'的值最大,DE'=5-1-2=2(cm).

　　如图
(4),当点M运动到点B'落在CD时,DB'(即
DE'')=$5-1-\sqrt{5}=(4-\sqrt{5})$cm,
　　　　　　
　
∴点E的运动轨迹为E→E'→E'',运动路径长=$2-\frac{3}{2}+2-(4-\sqrt{5})=(\sqrt{5}-\frac{3}{2})$cm