《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

24. 新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下：第八层楼房售价为4000元/平方米,从第八层起每上升一层,每平方米的售价提高50元；反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120平方米.
若购买者一次性付清所有房款,开发商有两种优惠方案：
方案一：降价$8\%$,另外每套楼房赠送$a$元装修基金；
方案二：降价$10\%$,没有其他赠送.
(1)请写出售价$y$(元/平方米)与楼层$x(1\leqslant x\leqslant23,x$取整数)之间的函数关系式；
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.

答案：
(1)当1≤x≤8时,每平方米的售价应为y=4000-(8-x)×30=30x+3760;当9≤x≤23时,每平方米的售价应为y=4000+(x-8)×50=50x+3600.
∴y=$\begin{cases}30x+3760(1\leqslant x\leqslant 8,\text{且}x\text{取整数}),\\50x+3600(9\leqslant x\leqslant 23,\text{且}x\text{取整数}).\end{cases}$
(2)第十六层楼房的每平方米的价格为50×16+3600=4400(元/平方米).按照方案一所交房款为W₁=4400×120×(1-8%)-a=(485760-a)元;按照方案二所交房款为W₂=4400×120×(1-10%)=475200(元).若W₁＞W₂,即485760-a＞475200,解得0＜a＜10560;若W₁=W₂时,即485760-a=475200,解得a=10560;若W₁＜W₂,即485760-a＜475200,解得a＞10560.
∴当0＜a＜10560时,方案二合算;当a=10560时,方案一与方案二一样;当a＞10560时,方案一合算.

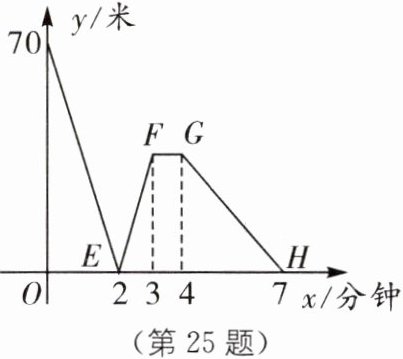
25. 新情境 机器人行走性能试验 有一科技小组进行了机器人行走性能试验,在试验场地有$A$,$B$,$C$三点顺次在同一笔直的赛道上,甲、乙两机器人分别从$A$,$B$两点同时同向出发,历时7分钟同时到达$C$点,乙机器人始终以60米/分钟的速度行走,如图是甲、乙两机器人之间的距离$y$(米)与他们的行走时间$x$(分钟)之间的函数图象,请结合图象,回答下列问题：
(1)$A$,$B$两点之间的距离是______米,甲机器人前2分钟的速度为______米/分钟；
(2)若前3分钟甲机器人的速度不变,求线段$EF$所在直线的函数关系式；
(3)若线段$FG// x$轴,则此段时间,甲机器人的速度为______米/分钟；
(4)求$A$,$C$两点之间的距离；
(5)在(2)和(3)的条件下,直接写出两机器人出发多长时间相距28米.

(1)7095
(2)线段EF所在直线的函数关系式为y=35x-70
(3)60
(4)A,C两点之间的距离为490米
(5)两机器人出发1.2分钟或2.8分钟或4.6分钟相距28米

答案：
(1)70 95 [解析]由图象可知,A,B两点之间的距离是70米,甲机器人前2分钟的速度为(70+60×2)÷2=95(米/分钟).
(2)设线段EF所在直线的函数关系式为y=kx+b.
∵1×(95-60)=35,
∴点F的坐标为(3,35).将点E(2,0),F(3,35)代入y=kx+b,得$\begin{cases}2k+b=0,\\3k+b=35,\end{cases}$解得$\begin{cases}k=35,\\b=-70.\end{cases}$故线段EF所在直线的函数关系式为y=35x-70.
(3)60 [解析]
∵线段FG//x轴,
∴甲、乙两机器人的速度都是60米/分钟.
(4)A,C两点之间的距离为70+60×7=490(米).
(5)两机器人出发x分钟相距28米.当0≤x＜2时,由题意,得60x+70-95x=28,解得x=1.2.当2≤x≤3时,由题意,得95x-60x-70=28,解得x=2.8.当4≤x≤7时,由直线GH经过点G(4,35)和点H(7,0),得直线GH的函数关系式为y=-$\frac{35}{3}$x+$\frac{245}{3}$.当y=28时,解得x=4.6.故两机器人出发1.2分钟或2.8分钟或4.6分钟相距28米.