《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

24. 阅读下列材料：
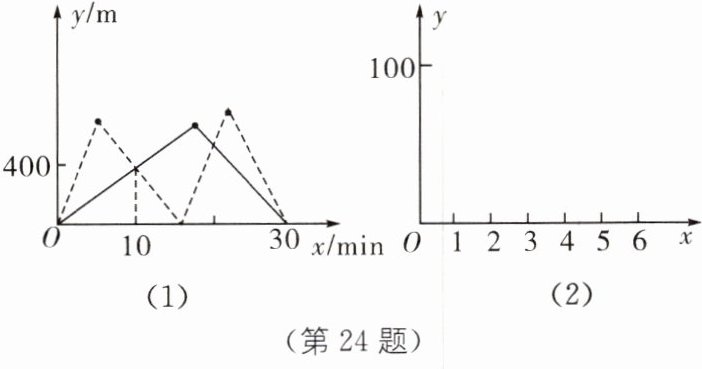
父亲和儿子同时出去晨练,如图(1),实线表示父亲离家的路程$y$($\mathrm { m }$)与时间$x$($\mathrm { min }$)的函数图象；虚线表示儿子离家的路程$y$($\mathrm { m }$)与时间$x$($\mathrm { min }$)的函数图象. 由图象可知,他们在出发$10 \mathrm { min }$时第一次相遇,此时离家$400 \mathrm { m }$；晨练了$30 \mathrm { min }$,他们同时到家.
根据阅读材料给你的启示,利用指定的直角坐标系(如图(2))或用其他方法解答问题：
一巡逻艇和一货轮同时从$A港口前往相距100 \mathrm { km }的B$港口,巡逻艇和货轮的速度分别为$100 \mathrm { km / h }和20 \mathrm { km / h }$,巡逻艇不停地往返于$A$,$B$两港口巡逻(巡逻艇调头的时间忽略不计).
(1)货轮从$A港口出发以后直到B$港口与巡逻艇一共相遇了几次?
(2)出发多少时间巡逻艇与货轮第三次相遇? 此时离$A$港口多少千米?

答案：
(1)4次
(2)设货轮从A港口出发的路程与时间的函数解析式为$y_1 = k_1x$，巡逻艇与货轮第三次相遇时的路程与时间的函数解析式为$y_2 = k_2x + b$。
货轮到达B港口所需时间为$\frac{100}{20} = 5\ \text{h}$，故$y_1 = k_1x$过点$(5, 100)$，可得$100 = 5k_1$，解得$k_1 = 20$，所以$y_1 = 20x$。
巡逻艇从A到B需$\frac{100}{100} = 1\ \text{h}$，从B到A需$1\ \text{h}$，则巡逻艇第二次到达B港口的时间为$3\ \text{h}$，第三次到达A港口的时间为$4\ \text{h}$，故$y_2 = k_2x + b$过点$(3, 100)$和$(4, 0)$，代入可得$\begin{cases}100 = 3k_2 + b \\ 0 = 4k_2 + b\end{cases}$，解得$\begin{cases}k_2 = -100 \\ b = 400\end{cases}$，所以$y_2 = -100x + 400$。
联立$\begin{cases}y = 20x \\ y = -100x + 400\end{cases}$，解得$20x = -100x + 400$，$120x = 400$，$x = \frac{10}{3}$。此时$y_1 = 20×\frac{10}{3} = \frac{200}{3}$。
故出发$\frac{10}{3}\ \text{h}$巡逻艇与货轮第三次相遇，离A港口$\frac{200}{3}\ \text{km}$。

25. 中考新考法 解题方法型阅读理解题 已知点$P ( x _ { 0 }, y _ { 0 } )和直线y = k x + b$,则点$P到直线y = k x + b的距离d可用公式d = \frac { | k x _ { 0 } - y _ { 0 } + b | } { \sqrt { 1 + k ^ { 2 } } }$计算.
例如：求点$P ( - 2, 1 )到直线y = x + 1$的距离.
解：因为直线$y = x + 1可变形为x - y + 1 = 0$,其中$k = 1$,$b = 1$,所以点$P ( - 2, 1 )到直线y = x + 1的距离d = \frac { | k x _ { 0 } - y _ { 0 } + b | } { \sqrt { 1 + k ^ { 2 } } } = \frac { | 1 × ( - 2 ) - 1 + 1 | } { \sqrt { 1 + 1 ^ { 2 } } } = \frac { 2 } { \sqrt { 2 } } = \sqrt { 2 }$.
根据以上材料,求：
(1)点$P ( 1, 1 )到直线y = 3 x - 2$的距离,并说明点$P$与直线的位置关系；
(2)点$P ( - 2, 1 )到直线y = 2 x - 1$的距离；
(3)已知直线$y = - x + 1与y = - x + 3$平行,求这两条直线的距离.

答案：
(1)因为直线$y = 3x - 2$可变形为$3x - y - 2 = 0$，其中$k = 3$，$b=-2$，所以点$P(1,1)$到直线$y = 3x - 2$的距离$d=\frac{|kx_0 - y_0 + b|}{\sqrt{1 + k^2}}=\frac{|3×1 - 1 + (-2)|}{\sqrt{1 + 3^2}}=\frac{0}{\sqrt{10}} = 0$。所以点$P(1,1)$在直线$y = 3x - 2$上。
(2)因为直线$y = 2x - 1$可变形为$2x - y - 1 = 0$，其中$k = 2$，$b=-1$，所以点$P(-2,1)$到直线$y = 2x - 1$的距离$d=\frac{|kx_0 - y_0 + b|}{\sqrt{1 + k^2}}=\frac{|2×(-2)-1 + (-1)|}{\sqrt{1 + 2^2}}=\frac{|-6|}{\sqrt{5}}=\frac{6\sqrt{5}}{5}$。
(3)因为直线$y=-x + 1$与$y=-x + 3$平行，取直线$y=-x + 1$上一点$P(0,1)$，直线$y=-x + 3$中$k=-1$，$b = 3$，则点$P(0,1)$到直线$y=-x + 3$的距离$d=\frac{|kx_0 - y_0 + b|}{\sqrt{1 + k^2}}=\frac{|-1×0 - 1 + 3|}{\sqrt{1 + (-1)^2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$，即两条直线的距离为$\sqrt{2}$。