2025年实验班提优训练暑假衔接版八升九年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
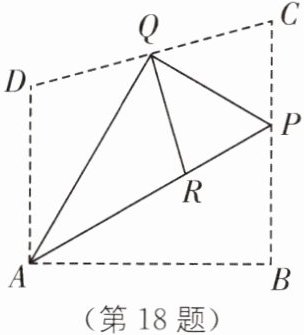
18. 中考新考法 操作探究 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片$ABCD沿过点A$的直线折叠,使得点$B落在CD上的点Q$处,折痕为$AP$;再将$\triangle PCQ$,$\triangle ADQ分别沿PQ$,$AQ$折叠,此时点$C$,$D落在AP上的同一点R$处.
请完成下列探究:
(1)$\angle PAQ$的大小为______$^{\circ}$;
(2)当四边形$APCD$是平行四边形时,$\frac{AB}{QR}$的值为______.
[答案]:(1)30 (2)$\sqrt{3}$
[解析](1)由折叠的性质,可得∠B=∠AQP,∠DAQ =∠QAP=∠PAB,∠DQA=∠AQR,∠CQP=∠PQR,∠D=∠ARQ,∠C=∠QRP.
∵∠QRA+∠QRP=180°,
∴∠D+∠C=180°,∴AD//BC,
∴∠B+∠DAB=180°.
∵∠RQD+∠RQC=180°,
∴∠RQA+∠RQP=90°,即∠AQP=90°,
∴∠B=∠AQP=90°,∴∠DAB=90°,
∴∠DAQ=∠QAP=∠PAB=30°.
(2)由折叠的性质,可得AD=AR,CP=PR.
∵四边形APCD是平行四边形,
∴AD=PC,∴AR=PR.
又∠AQP=90°,∴QR=$\frac{1}{2}$AP.
∵∠PAB=30°,∠B=90°,
∴AP=2PB,AB=$\sqrt{AP^2 - PB^2}=\sqrt{3}PB$,
∴PB=QR,∴$\frac{AB}{QR}=\sqrt{3}$18. 中考新考法 操作探究 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片$ABCD沿过点A$的直线折叠,使得点$B落在CD上的点Q$处,折痕为$AP$;再将$\triangle PCQ$,$\triangle ADQ分别沿PQ$,$AQ$折叠,此时点$C$,$D落在AP上的同一点R$处.
请完成下列探究:
(1)$\angle PAQ$的大小为__
(2)当四边形$APCD$是平行四边形时,$\frac{AB}{QR}$的值为__
请完成下列探究:
(1)$\angle PAQ$的大小为______$^{\circ}$;
(2)当四边形$APCD$是平行四边形时,$\frac{AB}{QR}$的值为______.

[答案]:(1)30 (2)$\sqrt{3}$
[解析](1)由折叠的性质,可得∠B=∠AQP,∠DAQ =∠QAP=∠PAB,∠DQA=∠AQR,∠CQP=∠PQR,∠D=∠ARQ,∠C=∠QRP.
∵∠QRA+∠QRP=180°,
∴∠D+∠C=180°,∴AD//BC,
∴∠B+∠DAB=180°.
∵∠RQD+∠RQC=180°,
∴∠RQA+∠RQP=90°,即∠AQP=90°,
∴∠B=∠AQP=90°,∴∠DAB=90°,
∴∠DAQ=∠QAP=∠PAB=30°.
(2)由折叠的性质,可得AD=AR,CP=PR.
∵四边形APCD是平行四边形,
∴AD=PC,∴AR=PR.
又∠AQP=90°,∴QR=$\frac{1}{2}$AP.
∵∠PAB=30°,∠B=90°,
∴AP=2PB,AB=$\sqrt{AP^2 - PB^2}=\sqrt{3}PB$,
∴PB=QR,∴$\frac{AB}{QR}=\sqrt{3}$18. 中考新考法 操作探究 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片$ABCD沿过点A$的直线折叠,使得点$B落在CD上的点Q$处,折痕为$AP$;再将$\triangle PCQ$,$\triangle ADQ分别沿PQ$,$AQ$折叠,此时点$C$,$D落在AP上的同一点R$处.
请完成下列探究:
(1)$\angle PAQ$的大小为__
30
__$^{\circ}$;(2)当四边形$APCD$是平行四边形时,$\frac{AB}{QR}$的值为__
$\sqrt{3}$
__.
答案:
(1)30
(2)$\sqrt{3}$
[解析]
(1)由折叠的性质,可得∠B=∠AQP,∠DAQ =∠QAP=∠PAB,∠DQA=∠AQR,∠CQP=∠PQR,∠D=∠ARQ,∠C=∠QRP.
∵∠QRA+∠QRP=180°,
∴∠D+∠C=180°,
∴AD//BC,
∴∠B+∠DAB=180°.
∵∠RQD+∠RQC=180°,
∴∠RQA+∠RQP=90°,即∠AQP=90°,
∴∠B=∠AQP=90°,
∴∠DAB=90°,
∴∠DAQ=∠QAP=∠PAB=30°.
(2)由折叠的性质,可得AD=AR,CP=PR.
∵四边形APCD是平行四边形,
∴AD=PC,
∴AR=PR.
又∠AQP=90°,
∴QR=$\frac{1}{2}$AP.
∵∠PAB=30°,∠B=90°,
∴AP=2PB,AB=$\sqrt{AP^2 - PB^2}=\sqrt{3}PB$,
∴PB=QR,
∴$\frac{AB}{QR}=\sqrt{3}$
(1)30
(2)$\sqrt{3}$
[解析]
(1)由折叠的性质,可得∠B=∠AQP,∠DAQ =∠QAP=∠PAB,∠DQA=∠AQR,∠CQP=∠PQR,∠D=∠ARQ,∠C=∠QRP.
∵∠QRA+∠QRP=180°,
∴∠D+∠C=180°,
∴AD//BC,
∴∠B+∠DAB=180°.
∵∠RQD+∠RQC=180°,
∴∠RQA+∠RQP=90°,即∠AQP=90°,
∴∠B=∠AQP=90°,
∴∠DAB=90°,
∴∠DAQ=∠QAP=∠PAB=30°.
(2)由折叠的性质,可得AD=AR,CP=PR.
∵四边形APCD是平行四边形,
∴AD=PC,
∴AR=PR.
又∠AQP=90°,
∴QR=$\frac{1}{2}$AP.
∵∠PAB=30°,∠B=90°,
∴AP=2PB,AB=$\sqrt{AP^2 - PB^2}=\sqrt{3}PB$,
∴PB=QR,
∴$\frac{AB}{QR}=\sqrt{3}$
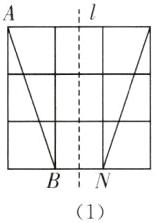
19. 图(1),(2),(3)都是$3×3$的正方形网络,每个小正方形的顶点称为格点,$A$,$B$,$C$均为格点. 在给定的网格中,按下列要求画图:
(1)在图(1)中,画一条不与$AB重合的线段MN$,使$MN与AB$关于某条直线对称,且$M$,$N$为格点;
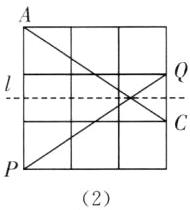
(2)在图(2)中,画一条不与$AC重合的线段PQ$,使$PQ与AC$关于某条直线对称,且$P$,$Q$为格点;
 (3)在图(3)中,画一个$\triangle DEF$,使$\triangle DEF与\triangle ABC$关于某条直线对称,且$D$,$E$,$F$为格点.
(3)在图(3)中,画一个$\triangle DEF$,使$\triangle DEF与\triangle ABC$关于某条直线对称,且$D$,$E$,$F$为格点.
(1)在图(1)中,画一条不与$AB重合的线段MN$,使$MN与AB$关于某条直线对称,且$M$,$N$为格点;
(2)在图(2)中,画一条不与$AC重合的线段PQ$,使$PQ与AC$关于某条直线对称,且$P$,$Q$为格点;
 (3)在图(3)中,画一个$\triangle DEF$,使$\triangle DEF与\triangle ABC$关于某条直线对称,且$D$,$E$,$F$为格点.
(3)在图(3)中,画一个$\triangle DEF$,使$\triangle DEF与\triangle ABC$关于某条直线对称,且$D$,$E$,$F$为格点.
答案:
(1)如图
(1),MN即为所求.
(2)如图
(2),PQ即为所求.
(3)如图
(3),△DEF即为所求.

(1)如图
(1),MN即为所求.
(2)如图
(2),PQ即为所求.
(3)如图
(3),△DEF即为所求.



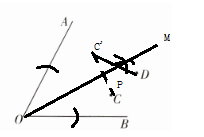
20. 如图,已知$\angle AOB和C$,$D$两点,求作一点$P使P到\angle AOB$两边的距离相等,且使$P到C$,$D$两点的距离和最小.


答案:

21. 如图,在$\triangle ABC$中,$\angle B= 90^{\circ}$,$AB= BD$,$AD= CD$,求$\angle CAD$的度数.
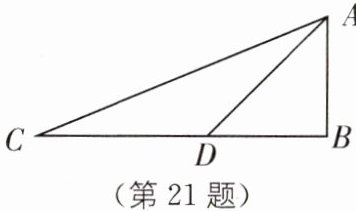

答案:
∵∠B=90°,AB=BD,
∴∠BAD=∠ADB=45°.
∵AD=CD,
∴∠DCA=∠CAD.
∴∠ADB=2∠CAD=45°.
∴∠CAD=22.5°.
∵∠B=90°,AB=BD,
∴∠BAD=∠ADB=45°.
∵AD=CD,
∴∠DCA=∠CAD.
∴∠ADB=2∠CAD=45°.
∴∠CAD=22.5°.
22. 如图,在$\triangle ABC$中,$\angle A= 60^{\circ}$,$BE$,$CF交于点P$,且分别平分$\angle ABC$,$\angle ACB$.
(1)求$\angle BPC$的度数;
(2)连接$EF$,求证:$\triangle EFP$是等腰三角形.
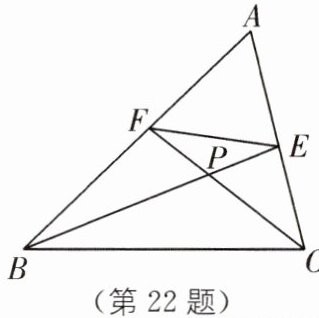
(1)求$\angle BPC$的度数;
(2)连接$EF$,求证:$\triangle EFP$是等腰三角形.

答案:
(1)
∵∠A=60°,
∴∠ABC+∠ACB=180°−∠A=120°.
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=$\frac{1}{2}$∠ABC,∠BCF=∠ACF=$\frac{1}{2}$∠ACB,
∴∠CBE+∠BCF=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}×120°=60°$,
∴∠BPC=180°−(∠CBE+∠BCF)=180°−60°=120°.
(2)如图,在BC上截取BQ=BF,连接PQ.

在△FBP和△QBP中,$\left\{\begin{array}{l}BP = BP\\∠FBP = ∠QBP\\BF = BQ\end{array}\right.$
∴△FBP≌△QBP(SAS),
∴FP=QP,∠BFP=∠BQP.
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360°−60°−120°=180°,
∴∠BFP+∠CEP=180°.
∵∠CQP+∠BQP=180°,
∴∠CEP=∠CQP.
在△CQP和△CEP中,$\left\{\begin{array}{l}∠QCP = ∠ECP\\∠CQP = ∠CEP\\CP = CP\end{array}\right.$
∴△CQP≌△CEP(AAS),
∴PE=QP.
∵FP=QP,
∴FP=EP,
∴△EFP是等腰三角形.
(1)
∵∠A=60°,
∴∠ABC+∠ACB=180°−∠A=120°.
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=$\frac{1}{2}$∠ABC,∠BCF=∠ACF=$\frac{1}{2}$∠ACB,
∴∠CBE+∠BCF=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}×120°=60°$,
∴∠BPC=180°−(∠CBE+∠BCF)=180°−60°=120°.
(2)如图,在BC上截取BQ=BF,连接PQ.

在△FBP和△QBP中,$\left\{\begin{array}{l}BP = BP\\∠FBP = ∠QBP\\BF = BQ\end{array}\right.$
∴△FBP≌△QBP(SAS),
∴FP=QP,∠BFP=∠BQP.
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360°−60°−120°=180°,
∴∠BFP+∠CEP=180°.
∵∠CQP+∠BQP=180°,
∴∠CEP=∠CQP.
在△CQP和△CEP中,$\left\{\begin{array}{l}∠QCP = ∠ECP\\∠CQP = ∠CEP\\CP = CP\end{array}\right.$
∴△CQP≌△CEP(AAS),
∴PE=QP.
∵FP=QP,
∴FP=EP,
∴△EFP是等腰三角形.
查看更多完整答案,请扫码查看


