2025年实验班提优训练暑假衔接版八升九年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
21. 如图,在 $ \triangle ABC $ 中,$ AD $ 是边 $ BC $ 的中线,点 $ M $ 在 $ AB $ 边上,点 $ N $ 在 $ AC $ 边上,并且 $ \angle MDN = 90^{\circ} $。若 $ BM^{2} + CN^{2} = DM^{2} + DN^{2} $,求证:$ AD^{2} = \frac{1}{4}(AB^{2} + AC^{2}) $。
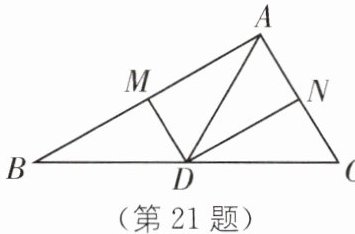

答案:
如图,延长ND到点P,使得DP=ND,连接BP,MP,MN.

∵AD是边BC的中线,
∴BD=CD.又∠BDP=∠CDN,
∴△BPD≌△CND(SAS).
∴BP=NC,PD=ND,∠DBP=∠C.
∴AC//BP.
∵$MN^{2}=DM^{2}+DN^{2}=BM^{2}+CN^{2}$,MD⊥PN,PD=ND,
∴MP=MN.
∴$MP^{2}=BM^{2}+BP^{2}$.
∴∠MBP=90°.
∴∠BAC=90°.在Rt△ABC中,$BC^{2}=AB^{2}+AC^{2}$,BC=2AD.
∴$(2AD)^{2}=AB^{2}+AC^{2}$.
∴$AD^{2}=\frac{1}{4}(AB^{2}+AC^{2})$.
如图,延长ND到点P,使得DP=ND,连接BP,MP,MN.

∵AD是边BC的中线,
∴BD=CD.又∠BDP=∠CDN,
∴△BPD≌△CND(SAS).
∴BP=NC,PD=ND,∠DBP=∠C.
∴AC//BP.
∵$MN^{2}=DM^{2}+DN^{2}=BM^{2}+CN^{2}$,MD⊥PN,PD=ND,
∴MP=MN.
∴$MP^{2}=BM^{2}+BP^{2}$.
∴∠MBP=90°.
∴∠BAC=90°.在Rt△ABC中,$BC^{2}=AB^{2}+AC^{2}$,BC=2AD.
∴$(2AD)^{2}=AB^{2}+AC^{2}$.
∴$AD^{2}=\frac{1}{4}(AB^{2}+AC^{2})$.
22. 如图,边长为 $ a $ 的正方形 $ ABCD $ 的四边贴着直线 $ l $ 向右无滑动“滚动”,当正方形“滚动”一周时,该正方形的中心 $ O $ 经过的路程是多少?顶点 $ A $ 经过的路程又是多少?
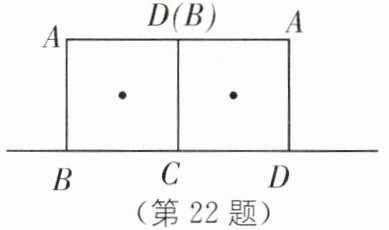

答案:
如图
(1),正方形ABCD“滚动”一周时,中心O所经过的路程为:

$L_{中}=\frac{1}{4}×2\pi(\frac{\sqrt{2}}{2}a)×4=\sqrt{2}\pi a$.
如图
(2),正方形ABCD“滚动”一周时,顶点A所经过的路程为:

$L_{顶}=\frac{1}{4}×2\pi(\sqrt{2}a)+2×\frac{1}{4}×2\pi a$=$\frac{1}{4}×2\sqrt{2}\pi a+2×\frac{1}{4}×2\pi a$=$\frac{2+\sqrt{2}}{2}\pi a$.
如图
(1),正方形ABCD“滚动”一周时,中心O所经过的路程为:

$L_{中}=\frac{1}{4}×2\pi(\frac{\sqrt{2}}{2}a)×4=\sqrt{2}\pi a$.
如图
(2),正方形ABCD“滚动”一周时,顶点A所经过的路程为:

$L_{顶}=\frac{1}{4}×2\pi(\sqrt{2}a)+2×\frac{1}{4}×2\pi a$=$\frac{1}{4}×2\sqrt{2}\pi a+2×\frac{1}{4}×2\pi a$=$\frac{2+\sqrt{2}}{2}\pi a$.
23. 如图,在五边形 $ A_{1}A_{2}A_{3}A_{4}A_{5} $ 中,$ B_{1},B_{2},B_{3},B_{4} $ 分别是 $ A_{1}A_{2},A_{2}A_{3},A_{3}A_{4},A_{4}A_{5} $ 的中点,$ M $ 是 $ B_{1}B_{3} $ 的中点,$ N $ 是 $ B_{2}B_{4} $ 的中点。若 $ A_{1}A_{5} = a $,求线段 $ MN $ 的长。


答案:
如图,连接$A_{2}A_{5}$,$A_{1}A_{4}$,取$A_{2}A_{5}$的中点O,连接$B_{1}O$,则$B_{1}O$平行且等于$\frac{1}{2}A_{1}A_{5}$,即$B_{1}O=\frac{a}{2}$.四边形$OB_{2}B_{3}B_{4}$为平行四边形,连接$OB_{3}$,可知$OB_{3}$必过$B_{2}B_{4}$的中点N.

∴$MN=\frac{1}{2}OB_{1}=\frac{a}{4}$.
如图,连接$A_{2}A_{5}$,$A_{1}A_{4}$,取$A_{2}A_{5}$的中点O,连接$B_{1}O$,则$B_{1}O$平行且等于$\frac{1}{2}A_{1}A_{5}$,即$B_{1}O=\frac{a}{2}$.四边形$OB_{2}B_{3}B_{4}$为平行四边形,连接$OB_{3}$,可知$OB_{3}$必过$B_{2}B_{4}$的中点N.

∴$MN=\frac{1}{2}OB_{1}=\frac{a}{4}$.
24. 如图,四边形 $ ABDE,ACFG $ 是 $ \triangle ABC $ 外侧的正方形,$ M $ 是 $ DF $ 的中点,$ MH \perp BC $ 于点 $ H $,求证:
(1)$ H $ 是 $ BC $ 的中点;
(2)$ MH = \frac{1}{2}BC $。
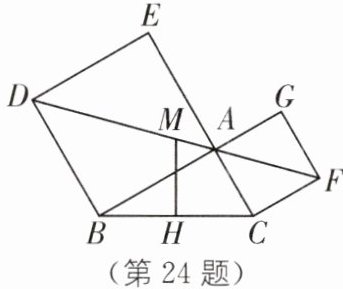
(1)$ H $ 是 $ BC $ 的中点;
(2)$ MH = \frac{1}{2}BC $。

答案:
(1)如图,过点D,A,F分别向直线BC作垂线,垂足是P,T,Q,易知∠1=∠2.

∴△BDP≌△ABT(AAS).
∴DP=BT,BP=AT.同理FQ=TC,CQ=AT.
∴PB=CQ.
∵M是DF的中点,
∴PH=HQ.
∴BH=PH-PB=HQ-CQ=HC,即H是BC的中点.
(2)
∵MH是梯形DPQF的中位线,
∴MH=$\frac{1}{2}(DP+FQ)=\frac{1}{2}(BT+TC)=\frac{1}{2}BC$.
(1)如图,过点D,A,F分别向直线BC作垂线,垂足是P,T,Q,易知∠1=∠2.

∴△BDP≌△ABT(AAS).
∴DP=BT,BP=AT.同理FQ=TC,CQ=AT.
∴PB=CQ.
∵M是DF的中点,
∴PH=HQ.
∴BH=PH-PB=HQ-CQ=HC,即H是BC的中点.
(2)
∵MH是梯形DPQF的中位线,
∴MH=$\frac{1}{2}(DP+FQ)=\frac{1}{2}(BT+TC)=\frac{1}{2}BC$.
查看更多完整答案,请扫码查看


